目录
前言
这篇文章主要介绍有关树和二叉树的知识。
树
定义
树是指==有n个结点的有限集==其逻辑结构为一对多的树形结构 在任意的一颗非空树种,有且仅有一个特定的结点称为——根 而n=0代表树为空 当n>1 时,其余结点又可分为互不相交的有限集,其中每一个集合本身又是一棵树,称为根的子树
如图所示——

这个图就能很好的表示出树的==递归==的概念
树的子树也是树……
基本术语
对于树这个比较新的概念,它有很多基本的术语需要我们了解 下面就介绍一些基本的术语
- 结点——树的基本组成单位,里面存放数据
- 双亲——除根结点以外,所有的结点都有连着上面的结点,称为其双亲
- 孩子——一个结点可能有向下连接着的结点,其称为这个结点的孩子结点
- 根节点——
- 非空树中无前驱的结点
- 兄弟——兄弟结点之间不相连,在同一层的结点,称为兄弟结点
- 堂兄弟——双亲在同一层的结点,且其双亲结点不同
- ==结点的==度——度是指这个结点拥有的==子树==个数
- 树的度——树内结点度的最大值
- 树的深度——
- ==树中结点的最大层次==
- 叶子结点——有双亲结点,没有孩子结点。是==树的终端结点==
- 有序树——树中的结点的各个子树从左往右有次序
- 无序树——树中的结点的各个子树无次序
- 森林——n个树的集合
二叉树
定义
对于树结构而言,树有一个双亲和多个孩子,而当限制孩子的个数时,树就变成了另外一种——==二叉树==
==二叉树==顾名思义是有两个孩子,意味着所有结点最多只能有两个子树
`那二叉树的定义究竟是什么呢? 二叉树是有n(n>=0)个元素的有限集,可以为空集,也可以是由一个根节点及两个互不相交的子树组成,这两个子树分别称为——左子树和右子树
🎄注意——二叉树不是树的特殊情况,它和树是两个概念,二叉树需要区分子树到底是左子树还是右子树,而树不用。
特殊二叉树
斜二叉树
对于二叉树而言结点是需要考虑是左子树还是右子树的,因此假如二叉树从根节点开始就沿着一个方向——都为左子树或者都为右子树
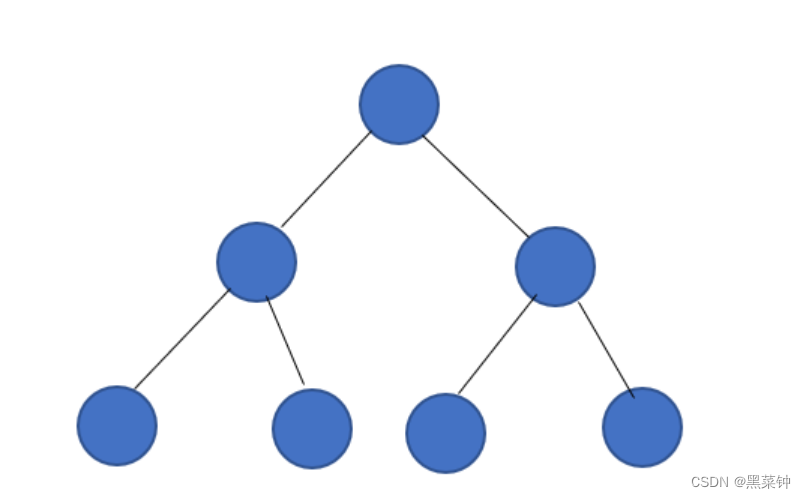
满二叉树
满二叉树就是指所有的结点的度都为2且其深度都相同的二叉树 看着也更为标准,每个结点的子树都满了,因此称为满二叉树。
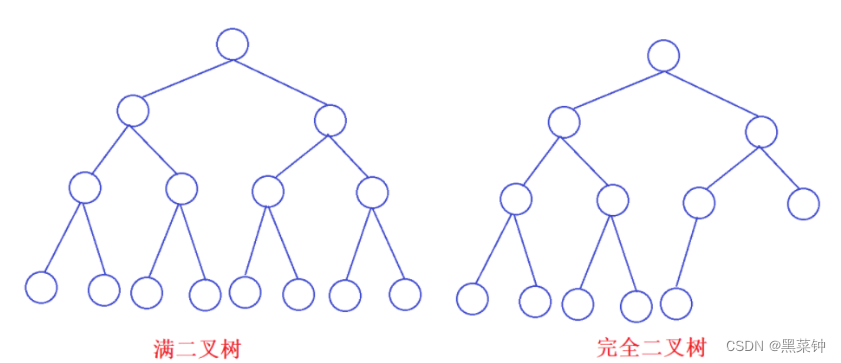
完全二叉树
完全二叉树就是和满二叉树的数据编号一致,只可能缺少几个右子树的叶子结点
具体的定义是——二叉树按照层序编码,在第i个的位置总是和对应的满二叉树的第i个结点的位置一样,则称为完全二叉树
显而易见,满二叉树也是一种特殊的完全二叉树
性质
基本二叉树的性质
- 性质1
- 第i层结点至多有2^(i-1)个
- 性质2
- 深度为k的树至多一共有2^k-1个结点
- 性质3
- 任何一颗二叉树的==叶子数=度为2的结点数+1==
- 从上往下看总边数B=结点数-1
- 从下往上看总边数B=2 * 度为2的结点+1 * 度为1的结点
- 而度为1的结点=结点总数-度为2的结点
- 所以——B两个式子联立,即可得这个式子
- 任何一颗二叉树的==叶子数=度为2的结点数+1==
其余二叉树性质
==性质4==
- 结点数为n的树,它的层数为[log2 n]+1
- [k]取不大于k的最大整数
- 推导——深度为k的结点数其最多有2^n-1个结点,至少要大于上一层(k-1层)的结点——2^(n-1)-1个
- 因此推导式子为==2^(n-1)-1<k<=2^n-1==
- 而k为整数,-1可以都省去了==2^(n-1)<k<=2^n==
- 化简即可得出结果
==性质5==
- 对于一颗有n个结点的完全二叉树的结点按照层序编号(从第一层开始到第[log2n]+1层,每层从左到右)对任意节点i都有——
1. 如果i=1,则结点i为二叉树的根,无双亲 ,如果i>1,其双亲结点为[i/2]
2. 若2i>n,则i结点无左孩子(当i为叶子结点时),否则其左孩子为2i
3. 若2i+1>n,则i结点无右孩子(当i为叶子结点时),否则其右孩子为2i+1
证明——

存储结构
存储结构也称为物理结构,之前的知识已经足够让我们掌握到这个的分类了 它分为==顺序存储结构==和==链式存储结构==
而链式存储又分为二叉链表和三叉链表
顺序存储
首先确定树存储的数据——树的结点的数据,利用下标来表示其层序顺序下的结点——but这里就出现了疑问——
对于不是满二叉树的其余二叉树而言,它们的编号和它们的子树的左右有关,只知道编号无法确定其位置——那如何解决这一个问题呢?
按照同层级的满二叉树的序列存放结点数据,对于没有的结点,存储为空
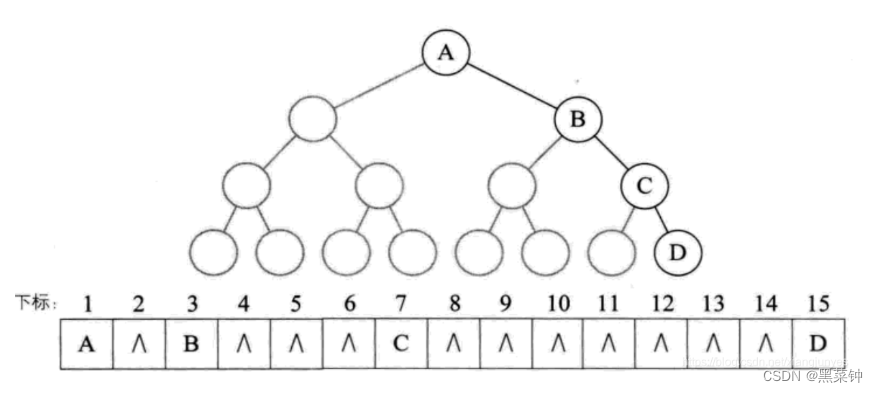
但是这会造成其内存的浪费,当二叉树为斜二叉树时,浪费的空间会很大,因此顺序存储结构主要用于完全二叉树
链式存储
二叉链表
链表中有两个指针域——1.指向左子树2.指向右子树
typedef struct Bitnode{
int data;
struct Bitnode * lchild ,* rchild;
}Bitnode,*Bittree;
三叉链表
链表中有三个指针域——1.指向左子树2.指向右子树3.指向双亲
typedef struct Bitnode{
int data;
struct Bitnode * lchild ,* rchild,* parent;
}Bitnode,*Bittree;
如图所示——  )
)
==遍历二叉树==
这个是二叉树操作的一切基础,很重要,其中的思想——递归也很重要,要重点注意。
从==根节点出发==依照一定的顺序一次访问二叉树中的每个结点,即为遍历二叉树 其中的访问,根据实际问题有不同的意思——但大体上都是对被访问的元素进行一系列操作,但一般不改变其值的大小
遍历方式
先序遍历(DLR)
先是指先遍历根,再遍历左子树,再遍历右子树 而左子树遍历也是先遍历左子树的根,再遍历这个左子树的左子树,最后是右子树,每个左子树和右子树要再进行一遍一系列同样的操作
——这就提及了一个重要的思想——递归
中序遍历(LDR)
先遍历左子树,再遍历根,再遍历右子树
后序遍历(LRD)
先遍历左子树,再遍历右子树,再遍历根
层次遍历
依照二叉树的层序序号,从左到右,从上到下依次遍历

遍历实现
递归实现
先序遍历算法(PreOrderTraverse)
c++
void PreOrderTraverse(Bittree b)
{
if(b==NULL)
{
return;//跳出并立刻结束所在方法的执行
}else
{
cout<<b->data<<endl;
PreOrderTraverse(b->lchild);
PreOrderTraverse(b->rchild);
}
}
中序遍历算法(InOrderTraverse)
c++
void InOrderTraverse(Bittree b)
{
if(b==NULL)
{
return;
}else
{
InOrderTraverse(b->lchild);
cout>>b->data>>endl;
InOrderTraverse(b->rchild);
}
}
后序遍历算法(PostOrderTraverse)
c++
void PostOrderTraverse(Bittree b)
{
if(b=NULL)
{
return;
}else
{
PostOrderTraverse(b->lchild);
PostOrderTraverse(b->rchild);
cout<<b->data<<endl;
}
}
非递归实现
利用栈来实现遍历——以中序遍历为例子
实际上,就是先把指针根节点入栈,然后遍历左子树,再把左子树看为一个二叉树,再把根节点入栈……直到该结点的左结点为空,则出栈,接着遍历该结点的右子树 ==出栈的一直都是根节点== ==栈空则结束==
c++
void FInOrderTraverse(Bittree b,Stack s,)
{
StackPush(&s,b);//先将头节点入栈
Bittree front=b;
while (!StackEmpty(&s))//栈不为空则继续
{
StackPush(&s);//头节点入栈
while(front)
{
StackPush(&s,front);
front=front->lchild;
}//最后指向的是结点的空的左子树
if (!StackEmpty(&s))
{
front = StackTop(&s);//若该节点左孩子为空,将其出栈,后找该节点右孩子
StackPop(&s);//出栈
cout<<front->a<<endl;
front = front->right;//后以同样的方法遍历右孩子
}
}
利用队列来实现——层次遍历
把根节点入队,然后如果其左右孩子不为0则根节点出队,其左孩子、右孩子分别入队,再让孩子出队,让孩子的孩子入队……直到左右孩子为0了,全部出队即可。
c++
void CcTraverse(Bittree b,Queue q)
{
if(b)//如果根不为空则
{
QueuePush(&q, b);//入队
}
while(!QueueEmpty(&q))//队列不为空继续进行
{
BTNode* front = QueueFront(&q);
QueuePop(&b);
cout<<front->data<<endl;
if(front->lchild)
{
QueuePush(&front->lchild);
}
if(front->rchild)
{
QueuePush(&front->rchild);
}
}
QueueDestory(&q);//销毁队列
}
遍历性质
已知前序遍历序列和中序遍历序列,可以唯一确定一颗二叉树 已知后序遍历序列和中序遍历序列,可以唯一确定一颗二叉树
遍历应用
建立二叉树
要建立任意一个普通二叉树之前,我们需要先确定其子树是左子树或是右子树 那么需要在原有二叉树的基础上加上几个无关结点——处理过后变为扩展二叉树
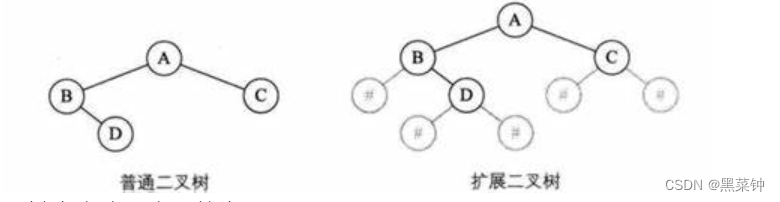
则其先序遍历序列就为AB#D##C## —— 判断是否为#,如果是则不创建结点 如果不是,则创建结点 其实本质上还是遍历——设定为某种序列 假如设置为先序序列,则在输入的字符不为#时就创建结点,先创建根节点,再创建左子树,再创建右子树
c++
void CreateBiTree(BiTree *T)
{
typeelem ch;
cin>>ch;
if(ch=="#")
{
*T=NULL;
}else
{
*T=new BiTNode;
if(!*T)
{
exit(OVERFLOW);
}
*T->data=ch;
CreateBiTree(&(*T)->lchild);
CreateBiTree(&(*T)->rchild);
}
}
线索二叉树
主要是在二叉树的基础上加上——可以指向前驱的域,利用二叉树中空着的指针域,让其指向这一节点的双亲
抽象数据类型定义
ADT BinaryTree{
//数据对象D:D是具有相同特性的数据元素的集合。
//数据关系R:
// 若D=Φ,则R=Φ,称BinaryTree为空二叉树;
// 若D≠Φ,则R={H},H是如下二元关系;
// (1)在D中存在惟一的称为根的数据元素root,它在关系H下无前驱;
// (2)若D-{root}≠Φ,则存在D-{root}={D1,Dr},且D1∩Dr =Φ;
// (3)若D1≠Φ,则D1中存在惟一的元素x1,<root,x1>∈H,且存在D1上的关系H1 ⊆H;若Dr≠Φ,则Dr中存在惟一的元素xr,<root,xr>∈H,且存在上的关系Hr ⊆H;H={<root,x1>,<root,xr>,H1,Hr};
// (4)(D1,{H1})是一棵符合本定义的二叉树,称为根的左子树;(Dr,{Hr})是一棵符合本定义的二叉树,称为根的右子树。
//基本操作:
InitBiTree( &T )
//操作结果:构造空二叉树T。
DestroyBiTree( &T )
// 初始条件:二叉树T已存在。
// 操作结果:销毁二叉树T。
CreateBiTree( &T, definition )
// 初始条件:definition给出二叉树T的定义。
// 操作结果:按definiton构造二叉树T。
ClearBiTree( &T )
// 初始条件:二叉树T存在。
// 操作结果:将二叉树T清为空树。
BiTreeEmpty( T )
// 初始条件:二叉树T存在。
// 操作结果:若T为空二叉树,则返回TRUE,否则返回FALSE。
BiTreeDepth( T )
// 初始条件:二叉树T存在。
// 操作结果:返回T的深度。
Root( T )
// 初始条件:二叉树T存在。
// 操作结果:返回T的根。
Value( T, e )
// 初始条件:二叉树T存在,e是T中某个结点。
// 操作结果:返回e的值。
Assign( T, &e, value )
// 初始条件:二叉树T存在,e是T中某个结点。
// 操作结果:结点e赋值为value。
Parent( T, e )
// 初始条件:二叉树T存在,e是T中某个结点。
// 操作结果:若e是T的非根结点,则返回它的双亲,否则返回“空”。
LeftChild( T, e )
// 初始条件:二叉树T存在,e是T中某个结点。
// 操作结果:返回e的左孩子。若e无左孩子,则返回“空”。
RightChild( T, e )
// 初始条件:二叉树T存在,e是T中某个结点。
// 操作结果:返回e的右孩子。若e无右孩子,则返回“空”。
LeftSibling( T, e )
// 初始条件:二叉树T存在,e是T中某个结点。
// 操作结果:返回e的左兄弟。若e是T的左孩子或无左兄弟,则返回“空”。
RightSibling( T, e )
// 初始条件:二叉树T存在,e是T中某个结点。
// 操作结果:返回e的右兄弟。若e是T的右孩子或无右兄弟,则返回“空”。
InsertChild( T, p, LR, c )
// 初始条件:二叉树T存在,p指向T中某个结点,LR为0或1,非空二叉树c与T不相交且右子树为空。
// 操作结果:根据LR为0或1,插入c为T中p所指结点的左或右子树。p所指结点的原有左或右子树则成为c的右子树。
DeleteChild( T, p, LR )
// 初始条件:二叉树T存在,p指向T中某个结点,LR为0或1。
// 操作结果:根据LR为0或1,删除T中p所指结点的左或右子树。
PreOrderTraverse( T, visit() )
// 初始条件:二叉树T存在,Visit是对结点操作的应用函数。
// 操作结果:先序遍历T,对每个结点调用函数Visit一次且仅一次。一旦visit()失败,则操作失败。
InOrderTraverse( T, visit() )
// 初始条件:二叉树T存在,Visit是对结点操作的应用函数。
// 操作结果:中序遍历T,对每个结点调用函数Visit一次且仅一次。一旦visit()失败,则操作失败。
PostOrderTraverse( T, visit() )
// 初始条件:二叉树T存在,Visit是对结点操作的应用函数。
// 操作结果:后序遍历T,对每个结点调用函数Visit一次且仅一次。一旦visit()失败,则操作失败。
LevelOrderTraverse( T, visit() )
// 初始条件:二叉树T存在,Visit是对结点操作的应用函数。
// 操作结果:层次遍历T,对每个结点调用函数Visit一次且仅一次。一旦visit()失败,则操作失败。
}ADT BinaryTree
树和森林
树的存储方式
双亲表示法
有一块区域存储双亲结点的下标 构造为结构数组,里面分别存放该结点的数值和双亲结点的下标
孩子链表表示法
构造一个数组 一块区域存放结点数据,一块区域存放指针——假如结点有孩子则存放左孩子的位置,然后如果有有右孩子,则在左孩子的指针域存放右孩子的地址
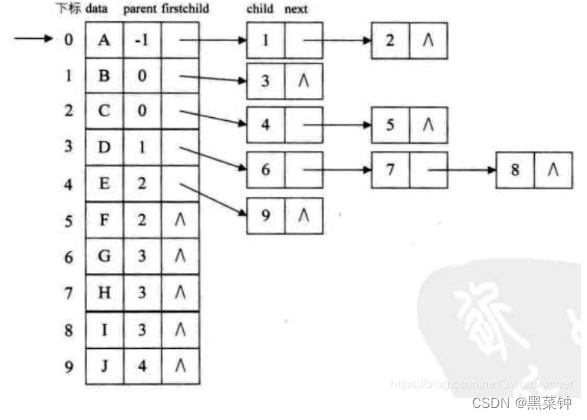
==孩子兄弟表示法==
这个把最常用,存储孩子和兄弟的结点
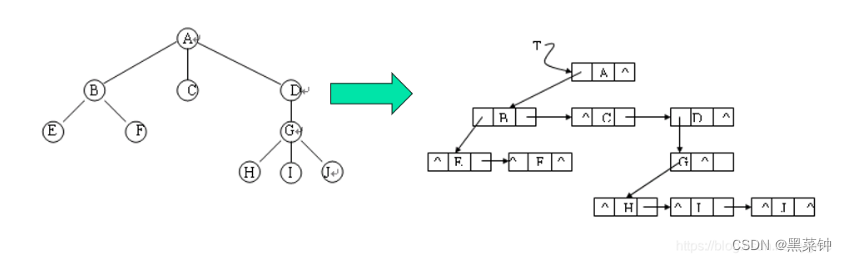
链式结构——有两个指针域分别存储第一个孩子的地址和兄弟的地址,如果没有孩子和兄弟,则为空
树和森林的遍历
树的3种遍历方式
- 先根遍历
先进行根结点——左孩子——其余孩子
c++
void PreOrderTraverse(Bittree b)
{
if(b! =NULL)
{
cout<<b->data<<endl;
PreOrderTraverse(b->lchild);
PreOrderTraverse(b->otherchild);
}
}
- 后跟遍历
先进行左孩子——其余孩子——根节点
c++
void HOrderTraverse(Bittree b)
{
if(b==NULL)
{
return;//跳出并立刻结束所在方法的执行
}else
{
HOrderTraverse(b->lchild);
cout<<b->data<<endl;
HOrderTraverse(b->otherchild);
}
}
- 层次遍历
依次从上往下,从左往右进行操作 这个需要构建队列来进行操作 代码如下:
c++
void CcTraverse(Bittree b,Queue q)
{
if(b)//如果根不为空则
{
QueuePush(&q, b);//入队
}
while(!QueueEmpty(&q))//队列不为空继续进行
{
BTNode* front = QueueFront(&q);
QueuePop(&b);
cout<<front->data<<endl;
if(front->lchild)
{
QueuePush(&front->lchild);
}
if(front->Otherchild)
{
QueuePush(&front->Otherchild);
}
}
QueueDestory(&q);//销毁队列
}
森林的遍历方式
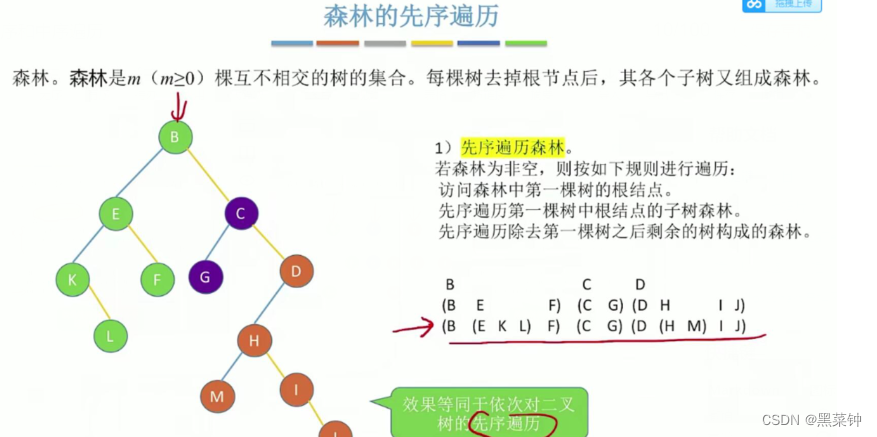
2.
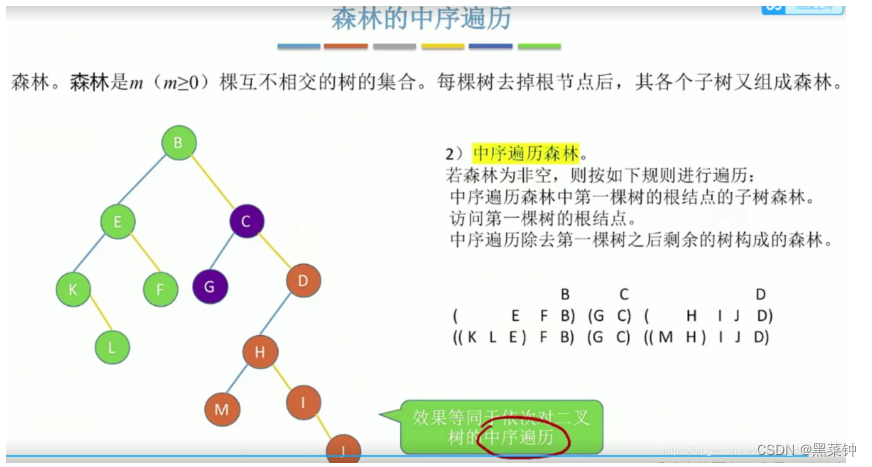
3.把森林转为二叉树,然后对二叉树进行先序或者中序遍历即得正确结果
树和森林的互相转换
树转换为二叉树
- 连接兄弟节点
- 把右边孩子结点与双亲结点连接的全部断开,只留左边孩子的结点与父母节点的联系
- 旋转一定角度,让二叉树看得较为规整
二叉树转换为树
- 所有的右孩子都与其双亲结点的双亲连接
- 删除其兄弟之间的连线
- 这个其实就是树转化为二叉树的逆过程
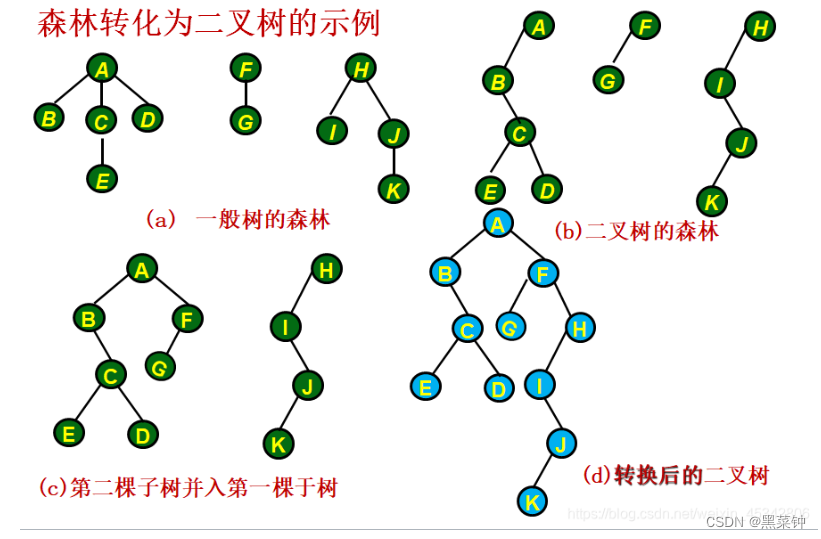
森林转化为二叉树
- 把森林中的每一颗树都转换为二叉树
- 然后把这些二叉树的根节点连接——其中一个作为根节点
哈夫曼树
引入
哈夫曼树是一种最优二叉树——什么最优呢?
这就需要我们知道一些概念了。
基本术语
- 结点间路径——结点间经过的结点和分支序列
- 结点的路径长度——从根节点到该结点路径上分支的数目
- 结点的权——在实际问题中,结点的被赋予一些特定的数值——具有某种意义,这些数值被称为结点的权值
- 结点的带权路径——从根节点到该结点的路径长度乘以该结点权值
- 树的带权路径——每个叶子结点的带权路径之和
哈夫曼树的概念
哈夫曼树就是二叉树中带权路径最短的
构造哈夫曼树——哈夫曼算法
理论
理论上就是让最远的权最大,最近的权最小 实际操作如图所示👇

- 首先把结点标号列出来 2.然后选取两个最小的合并 3.再以这个新合成的结点和其余结点作比较选择最小的两个 4.重复操作——再次合并 5.直到没有单个结点即可完成操作
代码实现
顺序存储,一维结构数组👇
c++
typedef struct{
int weight;
int parent,lch,rch;
}HTNode,*HuffmanTree;
假如哈夫曼树中有2n-1个结点不使用0下标,则数组大小为2n
c++
HuffmanTree ht=new HTNode[2n];
- 先把所有的双亲孩子设置为0;——==构造结点全是根==
- 生成n-1个结点——设置一个for循环,然后找到两个最小的结点
- 新合成的结点填在n+1上,并把其权值付给这个结点的权值域,孩子域也要填上其孩子节点的下标,且把这两个合并的结点的父母域填入合成节点的下标——相当于把这两个结点从独立的根节点给去除了,再次挑选最小结点时就不挑选这两个了
c++
void CreatHuffmanTree(HuffmanTree HT,int n)
{
if(n< =1) return;
m=2*n-1;
HT=new HTNode[m+1];
for(int i=1;i< =m;i++)
{
HT[i].lch=0;
HT[i].rch=0;
HT[i].parent=0;
}
for(i=1;i< =m;i++)
{
cin>> HT[i].weight;
}
for(i=n+1;i< =m;i++)
{
Select(HT,i-1,s1,s2);//在HT[k]中选择两个双亲为0的且其权值最小的结点,并返回其下标—s1和s2
HT[s1].parent=i;
HT[s2].parent=i;
HT[i].lch=s1;
HT[i].rch=s2;
HT[i].weight=HT[s1].weight+HT[s2].weight;
}
}
哈夫曼编码
- 在远程通讯中,要将待传字符转化为二进制编码
- ==由于其转换的本质是要设计长度不等的二进制编码,让待传字符串中出现字符较多的采用尽可能短的编码,则二进制编码的字符串便会减少==——而这时候就要用到哈夫曼编码来完成了
- 但是由于二进制编码只有0和1,容易导致字符转化回来的时候会发生错误——需要设计一种使任意字符的编码都不是另一字符的编码的前缀。——==前缀编码==
- 而使电文总长最短的前缀编码,则称为哈夫曼编码:由于哈夫曼树中没有一片树叶是另一片树叶的祖先,所以每个叶节点不可能是其余叶节点的前缀
方法——
- 统计字符出现的概率,概率越大的其编码越短
- 利用哈夫曼树的特点:权越大离根节点越近
- 在哈夫曼树的每个分支标0/1——左分支标0,右分支标1
- 从跟到叶子的路径编号连起来,作为叶子代表的字符编码
代码实现:
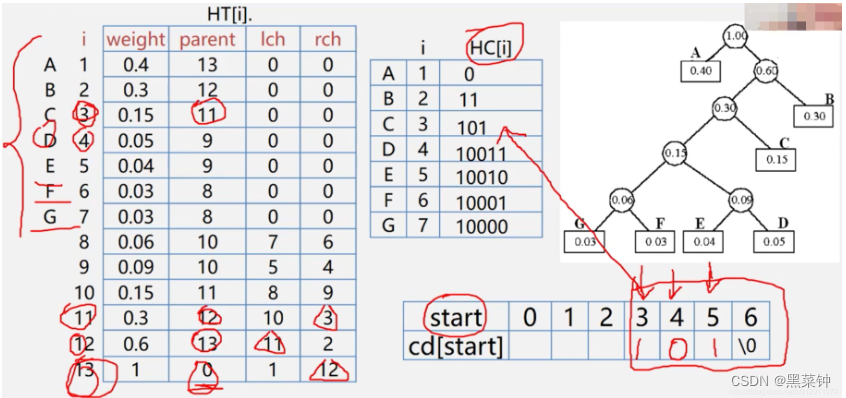
需要构造三个空间分别存储哈夫曼树、哈夫曼编码、每一个结点的每一位编码存储
c++
void HuffmanCode(Node *p, const int numLeafs, string *codes) {
// p为节点数组的指针,codes为string数组的指针
// 用于存储每个节点的哈夫曼码
// parent表示父节点位置
int parent;
// 每次对一个叶子节点进行编码
// i表示当前叶子节点位置
for (int i=0; i < numLeafs; i++) {
// j表示当前节点位置,i是不能在下面循环中改变的
// 使用j来记录节点的移动过程
int j = i;
// 当前节点的父节点位置
parent = p[i].parent;
// 从当前叶子节点p[i]开始,找到哈夫曼树的根节点
// 循环结束条件是此时parent为0,即达到哈夫曼树的根节点
while(parent ! = -1) {
if (p[parent].left == j) {[
// 如果当前节点是父节点的左子树,则此分支编码为0
codes[i].push_back('0');
}
// 如果当前节点是父节点的右子树,则编码为1
else {
codes[i].push_back('1');
}
j = parent;
parent = p[j].parent;
}
cout << codes[i] << endl;
}
}










