0
点赞
收藏
分享

微信扫一扫

React——react 的基本使用

西风白羽 03-18 08:30 阅读 5
人工智能pytorchcomputer vision计算机视觉

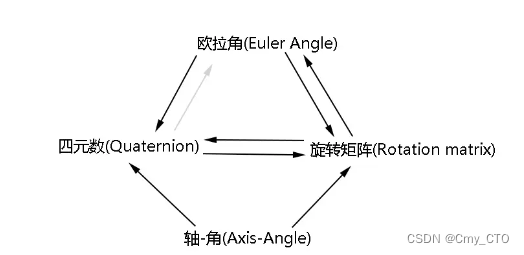
Rotation Representations Transformation

在这里插入图片描述

Euler Angles to Rotation Matrix

旋转角度(α,β,γ),旋转顺序(z->y->x),外旋.

可以写为:
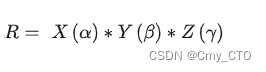
公式a
[ 公式a ]

其中:
在这里插入图片描述
这个公式(a)根据旋转矩阵构成的定义即可得到.

而上述(α,β,γ),旋转顺序(x->y->z),内旋.

可以写为:

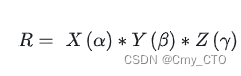
在这里插入图片描述

[公式b]

这个公式的推导稍微复杂些,这里只给出定义,推导过程不在本文的探讨范围内.

可以发现, 公式(a)与公式(b)是一样的.也就是说x->y->z内旋等价于z->y->x,外旋.

事实上,每种特定顺序的外旋等价于其相反顺序的内旋.

Rotation Matrix to Euler Angles

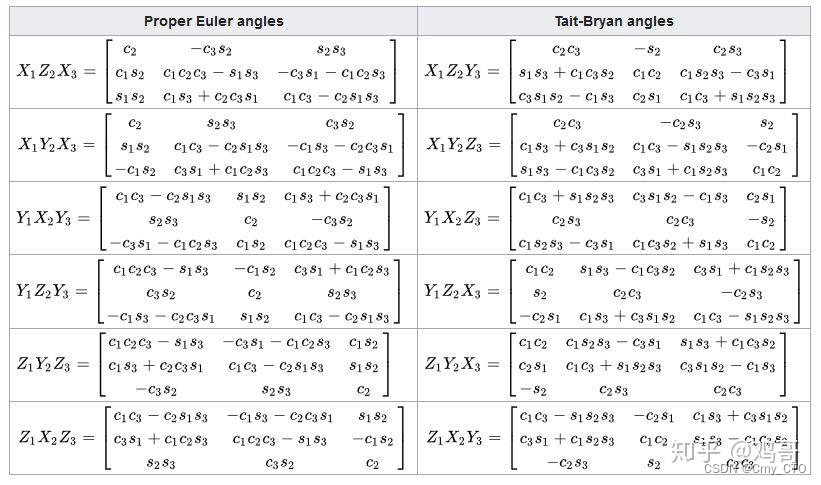
在这里插入图片描述

在这里插入图片描述
这张表描述了所有旋转的组合.以最后一行为例,我们可以把这里的 Z1X2Y3认为是Z->X->Y内旋 or Y->X->Z外旋.

从矩阵的角度就是ZXY.

这里的1,2,3可以认为是各个转轴上的旋转角度.后面的c1表示cos(绕Z轴转角).s1表示sin(绕Z轴转角).

旋转矩阵转欧拉角可以结合这张表中的公式. 比如对一个给定的旋转矩阵R.我们需要把R分解为ZXY形式的欧拉角.我们就找到最后一行的 Z1X2Y3 .我们记Z,X,Y对应的角度分别为yaw,roll,pitch.而

sin(yaw) = s1, cos(yaw) = c1.

sin(roll) = s2, cos(roll) = c2.

sin(pitch) = s3, cos(pitch) = c3.

我们的计算方式是寻找每个角度对应的tan值.

我们看到R[0][1]/R[1][1] = (-c2s1)/(c1c2) = -s1/c1 = -tan1.

则yaw = -atan2(R[0][1]/R[1][1]).

我们知道了yaw, 就能计算出c1, s1, 代入R[1][1] = c1c2可以求出c2.

c2结合R[2][1]=s2可计算出tan2, 得到roll.

同样的方法,得到tan3, 计算出pitch.

至此可得yaw,roll,pitch.

一般情况下可以如此计算,不过在万向节思索状态下似乎会出现分母为0的情况.

Quaternion to Rotation Matrix

众所周知的是，欧拉旋转是有万向节死锁(Gimbal Lock)的问题的。幸好我们有四元数(Quaternion)这种数学工具可以避免这个情况。一般来说，我们都会用单位四元数q=w+xi+yj+zk 来表示旋转，其中 ||q|| = x2+y2+z2+w2=1。
那么给定一个单位四元数，可以构造旋转矩阵(column major)[1][4][8][14][15]：
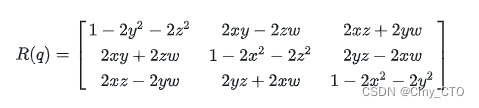
在这里插入图片描述
这个四元数构造的大概思路就是把四元数的旋转操作写成矩阵形式
注：给定一个用于旋转的单位四元数 q=w+xi+yj+zk 和被旋转的三维向量 v ，那么要直接用四元数旋转这个向量，则我们首先要构造一个纯四元数 p = (v,0) ，设旋转后的向量为 v’ ，旋转后的向量构造的纯四元数为 p’ = (v’,0) ，那么 p’ =qpq-1 。
因为是用四元数来构造矩阵的，所以这个矩阵构造公式就没有欧拉角顺规的说法了。

Rotation Matrix to Quaternion

那第一步肯定是判断3x3矩阵是一个正交矩阵啦（满足 RRT = RTR = I）。
那么如果这个矩阵已经是一个合法的旋转矩阵了，要从旋转矩阵里提取四元数，也是可以像提取欧拉角那样，用参数化过的矩阵的表达式凑出来。参考[8]《Real Time Rendering 3rd edition》Chapter4的思路，我们观察一下用四元数分量进行参数化的矩阵 R(q) ，然后经过一顿操作，我们发现：

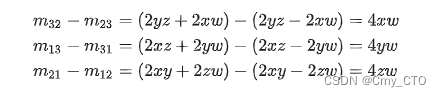
在这里插入图片描述
于是我们再凑出个实分量w ，就可以把四元数四个分量都用矩阵元素表示出来了。于是我们又机智地发现了一个等式：
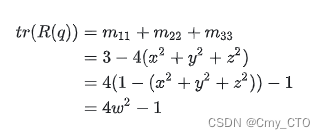
在这里插入图片描述
其中 tr(M) 是矩阵 M 的迹(trace)，也就是矩阵对角元素的和。因为这里用的是3x3矩阵，跟其他资料里面的表示有一点不同。所以我们可以把四元数的四个分量都用矩阵元素凑出来了：
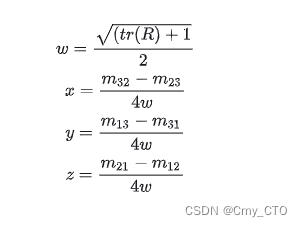
在这里插入图片描述
绝对值比较小的时候，可能会出现数值不稳定的情况，那么想要数值稳定的话就得用一种不用除法的方式来凑

Euler Angles to Quaternion

四元数的乘积
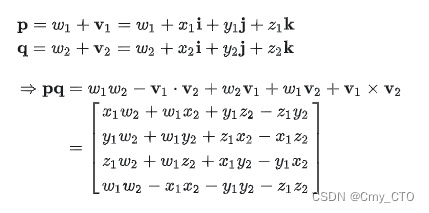
在这里插入图片描述
欧拉角构造四元数，跟欧拉角构造旋转矩阵一样，就是把三个基础旋转Elemental Rotation组合在一起。

那么用于旋转的四元数 q(x,y,z,w) 的表达式是：
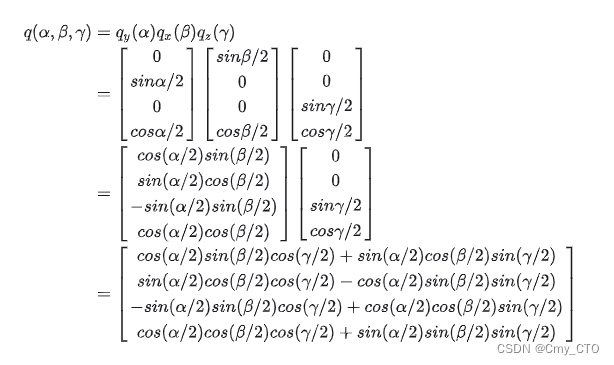
在这里插入图片描述

Quaternion to Euler Angles

本以为，从四元数提取欧拉角的思路可以跟旋转矩阵提取欧拉角类似，也是用四元数的元素运算和反三角函数凑出公式来。
后来发现这简直就是一个极其硬核的任务，展开之后每一项都是六次多项式，画面有一丢暴力且少儿不宜，直接强行凑的话画风大概是这样：

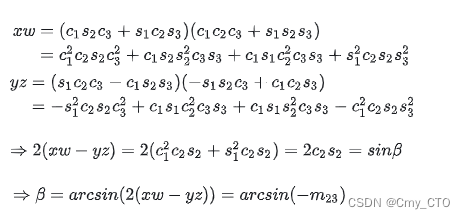
在这里插入图片描述
这个结果跟欧拉角参数化的旋转矩阵表达式是吻合的。
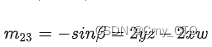
在这里插入图片描述

但这还只是最好凑的那一个，惹不起惹不起。所以舒服的思路还是四元数–>旋转矩阵–>欧拉角，想一步到位的话，把四元数分量参数化的旋转矩阵、欧拉角参数化的旋转矩阵结合在一起，参考下旋转矩阵转欧拉角的方法，替换下元素就完事了。这里就不把公式展开了，因为四元数直接转欧拉角 跟 旋转矩阵转欧拉角一样，依旧是要处理gimbal lock的corner case，还是那么麻烦，

Axis-Angle to Quaternion

轴-角(Axis-Angle)顾名思义就是绕某条单位轴旋转一定角度，从这个意义上看，它构造四元数是非常舒服的，毕竟直观的几何意义有一点点类似，绕单位轴 u 旋转 θ的四元数是：
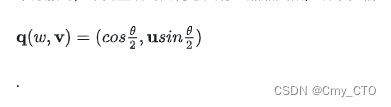
在这里插入图片描述

Quaternion to Axis-Angle

设四元数q = q0+q1i+q2j+q3k对应的轴角为（θ,k），其中k=(k1,k2,k3)。则四元数到轴角的转换为：

θ = 2 arccos q0
[k1, k2, k3]T = [q1, q2, q3]T / sin(θ/2)

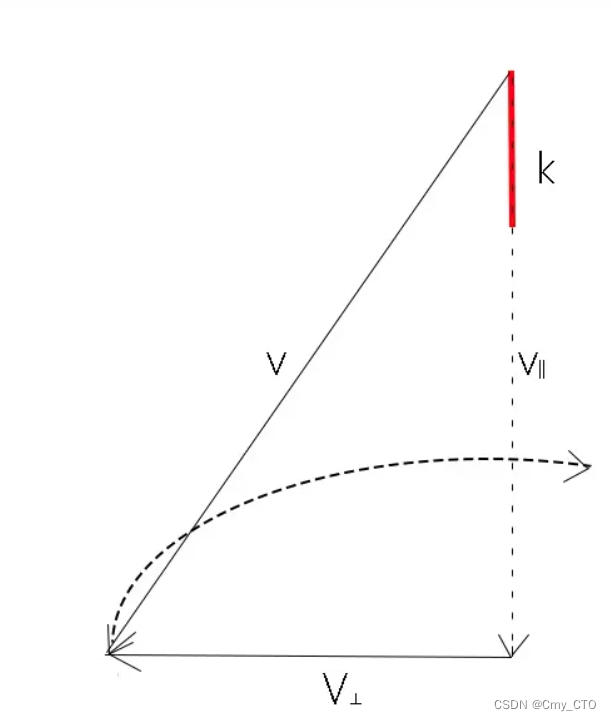
Axis-Angle to Rotation Matrix

Axis Angle转Rotation Matrix可以从罗德里格斯旋转公式Rodrigues Rotation Formula开始推导。
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

Code

tf

from tf import transformations
import math
import numpy a3s np

def euler_to_matrix_rad(x, y, z):
    T = transformations.euler_matrix(x, y, z, "sxyz")
    return T

def matrix_to_euler_rad(matrix):
    q = transformations.quaternion_from_matrix(matrix)
    eulers = transformations.euler_from_quaternion(q, axes='sxyz')
    return eulers

def matrix_to_quaternion(matrix):
    return transformations.quaternion_from_matrix(matrix)

#四元数是ijk3 也就是xyz的顺序
def quaternion_to_matrix(quat):
    return transformations.quaternion_matrix(quat)

def quaternion_to_euler_rad(quat):
    return transformations.euler_from_quaternion(quat, axes='sxyz')

def euler_to_quaternion_rad(x, y, z):
    return transformations.quaternion_from_euler(x, y, z, axes='sxyz')

def rad_to_degree(rad):
    return rad / math.pi * 180

def degree_to_euler(degree):
    return degree / 180 * math.pi

def inverse_matrix(matrix):
    return transformations.inverse_matrix(matrix)

#注意简单的a*b是按对应位置元素相乘
def dot_matrix(a, b):
  return np.dot(a, b)

pytorch3d

install

  • conda env install
conda install pytorch3d -c pytorch3d
  • Install from GitHub
pip install "git+https://github.com/facebookresearch/pytorch3d.git"
  • Install from a local clone
git clone https://github.com/facebookresearch/pytorch3d.git
cd pytorch3d && pip install -e .

要在从本地克隆运行安装后重建，请rm-rf build/**/*.然后pip install -e。在重新安装PyTorch之后，通常需要重建pytorch3d。
对于版本早于CUDA 11的CUDA构建，如上所述，在构建之前设置CUB_HOME。

test installation

python3 -m unittest discover -v -s tests -t .

Use

不同旋转表示方式之间的转换在网上可以找到很多相关的代码，同时也有一些库帮助我们实现了它们之间的转换，
比如
python里的scipy包，其旋转相关的转换代码在scipy.spatial.transform里面，**C++**里则可以使用Eigen库来实现
pytorch里，则可以使用pytorch3d包
在pytorch3d的transforms模块里，实现了丰富的（甚至还有2019年CVPR上提出的6d表示方式的转换）旋转表示方式之间的转换，而且都是batch形式的，对于深度学习非常友好方便。

pytorch3d.transforms模块

Code
axis_angle_to_matrix,            # 轴角转旋转矩阵
axis_angle_to_quaternion,        # 轴角转四元数
euler_angles_to_matrix,          # 欧拉角转旋转矩阵
matrix_to_euler_angles,          # 旋转矩阵转欧拉角
matrix_to_quaternion,            # 旋转矩阵转四元数
matrix_to_rotation_6d,           # 旋转矩阵转6d表示
quaternion_apply,                # 使用四元数对三维点进行旋转
quaternion_invert,               # 求四元数旋转的逆
quaternion_multiply,             # 组合两次四元数旋转为一个四元数
quaternion_raw_multiply,         # 同上一样
quaternion_to_axis_angle,        # 四元数转轴角
quaternion_to_matrix,            # 四元数转旋转矩阵
random_quaternions,              # 生成随机四元数
random_rotation,                 # 生成随机旋转矩阵
random_rotations,                # 同上一样
rotation_6d_to_matrix,           # 6d表示转旋转矩阵
standardize_quaternion,          # 将一个单位四元数转换为标准形式(实部≥0)

Code

# Copyright (c) Facebook, Inc. and its affiliates.
# All rights reserved.
#
# This source code is licensed under the BSD-style license found in the
# LICENSE file in the root directory of this source tree.

import functools
from typing import Optional

import torch
import torch.nn.functional as F

from ..common.types import Device


"""
The transformation matrices returned from the functions in this file assume
the points on which the transformation will be applied are column vectors.
i.e. the R matrix is structured as

    R = [
            [Rxx, Rxy, Rxz],
            [Ryx, Ryy, Ryz],
            [Rzx, Rzy, Rzz],
        ]  # (3, 3)

This matrix can be applied to column vectors by post multiplication
by the points e.g.

    points = [[0], [1], [2]]  # (3 x 1) xyz coordinates of a point
    transformed_points = R * points

To apply the same matrix to points which are row vectors, the R matrix
can be transposed and pre multiplied by the points:

e.g.
    points = [[0, 1, 2]]  # (1 x 3) xyz coordinates of a point
    transformed_points = points * R.transpose(1, 0)
"""


def quaternion_to_matrix(quaternions):
    """
    Convert rotations given as quaternions to rotation matrices.

    Args:
        quaternions: quaternions with real part first,
            as tensor of shape (..., 4).

    Returns:
        Rotation matrices as tensor of shape (..., 3, 3).
    """
    r, i, j, k = torch.unbind(quaternions, -1)
    two_s = 2.0 / (quaternions * quaternions).sum(-1)

    o = torch.stack(
        (
            1 - two_s * (j * j + k * k),
            two_s * (i * j - k * r),
            two_s * (i * k + j * r),
            two_s * (i * j + k * r),
            1 - two_s * (i * i + k * k),
            two_s * (j * k - i * r),
            two_s * (i * k - j * r),
            two_s * (j * k + i * r),
            1 - two_s * (i * i + j * j),
        ),
        -1,
    )
    return o.reshape(quaternions.shape[:-1] + (3, 3))


def _copysign(a, b):
    """
    Return a tensor where each element has the absolute value taken from the,
    corresponding element of a, with sign taken from the corresponding
    element of b. This is like the standard copysign floating-point operation,
    but is not careful about negative 0 and NaN.

    Args:
        a: source tensor.
        b: tensor whose signs will be used, of the same shape as a.

    Returns:
        Tensor of the same shape as a with the signs of b.
    """
    signs_differ = (a < 0) != (b < 0)
    return torch.where(signs_differ, -a, a)


def _sqrt_positive_part(x: torch.Tensor) -> torch.Tensor:
    """
    Returns torch.sqrt(torch.max(0, x))
    but with a zero subgradient where x is 0.
    """
    ret = torch.zeros_like(x)
    positive_mask = x > 0
    ret[positive_mask] = torch.sqrt(x[positive_mask])
    return ret


def matrix_to_quaternion(matrix: torch.Tensor) -> torch.Tensor:
    """
    Convert rotations given as rotation matrices to quaternions.

    Args:
        matrix: Rotation matrices as tensor of shape (..., 3, 3).

    Returns:
        quaternions with real part first, as tensor of shape (..., 4).
    """
    if matrix.size(-1) != 3 or matrix.size(-2) != 3:
        raise ValueError(f"Invalid rotation matrix  shape f{matrix.shape}.")

    batch_dim = matrix.shape[:-2]
    m00, m01, m02, m10, m11, m12, m20, m21, m22 = torch.unbind(
        matrix.reshape(*batch_dim, 9), dim=-1
    )

    q_abs = _sqrt_positive_part(
        torch.stack(
            [
                1.0 + m00 + m11 + m22,
                1.0 + m00 - m11 - m22,
                1.0 - m00 + m11 - m22,
                1.0 - m00 - m11 + m22,
            ],
            dim=-1,
        )
    )

    # we produce the desired quaternion multiplied by each of r, i, j, k
    quat_by_rijk = torch.stack(
        [
            torch.stack([q_abs[..., 0] ** 2, m21 - m12, m02 - m20, m10 - m01], dim=-1),
            torch.stack([m21 - m12, q_abs[..., 1] ** 2, m10 + m01, m02 + m20], dim=-1),
            torch.stack([m02 - m20, m10 + m01, q_abs[..., 2] ** 2, m12 + m21], dim=-1),
            torch.stack([m10 - m01, m20 + m02, m21 + m12, q_abs[..., 3] ** 2], dim=-1),
        ],
        dim=-2,
    )

    # We floor here at 0.1 but the exact level is not important; if q_abs is small,
    # the candidate won't be picked.
    # pyre-ignore [16]: `torch.Tensor` has no attribute `new_tensor`.
    quat_candidates = quat_by_rijk / (2.0 * q_abs[..., None].max(q_abs.new_tensor(0.1)))

    # if not for numerical problems, quat_candidates[i] should be same (up to a sign),
    # forall i; we pick the best-conditioned one (with the largest denominator)

    return quat_candidates[
        F.one_hot(q_abs.argmax(dim=-1), num_classes=4) > 0.5, :  # pyre-ignore[16]
    ].reshape(*batch_dim, 4)


def _axis_angle_rotation(axis: str, angle):
    """
    Return the rotation matrices for one of the rotations about an axis
    of which Euler angles describe, for each value of the angle given.

    Args:
        axis: Axis label "X" or "Y or "Z".
        angle: any shape tensor of Euler angles in radians

    Returns:
        Rotation matrices as tensor of shape (..., 3, 3).
    """

    cos = torch.cos(angle)
    sin = torch.sin(angle)
    one = torch.ones_like(angle)
    zero = torch.zeros_like(angle)

    if axis == "X":
        R_flat = (one, zero, zero, zero, cos, -sin, zero, sin, cos)
    if axis == "Y":
        R_flat = (cos, zero, sin, zero, one, zero, -sin, zero, cos)
    if axis == "Z":
        R_flat = (cos, -sin, zero, sin, cos, zero, zero, zero, one)

    return torch.stack(R_flat, -1).reshape(angle.shape + (3, 3))


def euler_angles_to_matrix(euler_angles, convention: str):
    """
    Convert rotations given as Euler angles in radians to rotation matrices.

    Args:
        euler_angles: Euler angles in radians as tensor of shape (..., 3).
        convention: Convention string of three uppercase letters from
            {"X", "Y", and "Z"}.

    Returns:
        Rotation matrices as tensor of shape (..., 3, 3).
    """
    if euler_angles.dim() == 0 or euler_angles.shape[-1] != 3:
        raise ValueError("Invalid input euler angles.")
    if len(convention) != 3:
        raise ValueError("Convention must have 3 letters.")
    if convention[1] in (convention[0], convention[2]):
        raise ValueError(f"Invalid convention {convention}.")
    for letter in convention:
        if letter not in ("X", "Y", "Z"):
            raise ValueError(f"Invalid letter {letter} in convention string.")
    matrices = map(_axis_angle_rotation, convention, torch.unbind(euler_angles, -1))
    return functools.reduce(torch.matmul, matrices)


def _angle_from_tan(
    axis: str, other_axis: str, data, horizontal: bool, tait_bryan: bool
):
    """
    Extract the first or third Euler angle from the two members of
    the matrix which are positive constant times its sine and cosine.

    Args:
        axis: Axis label "X" or "Y or "Z" for the angle we are finding.
        other_axis: Axis label "X" or "Y or "Z" for the middle axis in the
            convention.
        data: Rotation matrices as tensor of shape (..., 3, 3).
        horizontal: Whether we are looking for the angle for the third axis,
            which means the relevant entries are in the same row of the
            rotation matrix. If not, they are in the same column.
        tait_bryan: Whether the first and third axes in the convention differ.

    Returns:
        Euler Angles in radians for each matrix in data as a tensor
        of shape (...).
    """

    i1, i2 = {"X": (2, 1), "Y": (0, 2), "Z": (1, 0)}[axis]
    if horizontal:
        i2, i1 = i1, i2
    even = (axis + other_axis) in ["XY", "YZ", "ZX"]
    if horizontal == even:
        return torch.atan2(data[..., i1], data[..., i2])
    if tait_bryan:
        return torch.atan2(-data[..., i2], data[..., i1])
    return torch.atan2(data[..., i2], -data[..., i1])


def _index_from_letter(letter: str):
    if letter == "X":
        return 0
    if letter == "Y":
        return 1
    if letter == "Z":
        return 2


def matrix_to_euler_angles(matrix, convention: str):
    """
    Convert rotations given as rotation matrices to Euler angles in radians.

    Args:
        matrix: Rotation matrices as tensor of shape (..., 3, 3).
        convention: Convention string of three uppercase letters.

    Returns:
        Euler angles in radians as tensor of shape (..., 3).
    """
    if len(convention) != 3:
        raise ValueError("Convention must have 3 letters.")
    if convention[1] in (convention[0], convention[2]):
        raise ValueError(f"Invalid convention {convention}.")
    for letter in convention:
        if letter not in ("X", "Y", "Z"):
            raise ValueError(f"Invalid letter {letter} in convention string.")
    if matrix.size(-1) != 3 or matrix.size(-2) != 3:
        raise ValueError(f"Invalid rotation matrix  shape f{matrix.shape}.")
    i0 = _index_from_letter(convention[0])
    i2 = _index_from_letter(convention[2])
    tait_bryan = i0 != i2
    if tait_bryan:
        central_angle = torch.asin(
            matrix[..., i0, i2] * (-1.0 if i0 - i2 in [-1, 2] else 1.0)
        )
    else:
        central_angle = torch.acos(matrix[..., i0, i0])

    o = (
        _angle_from_tan(
            convention[0], convention[1], matrix[..., i2], False, tait_bryan
        ),
        central_angle,
        _angle_from_tan(
            convention[2], convention[1], matrix[..., i0, :], True, tait_bryan
        ),
    )
    return torch.stack(o, -1)


def random_quaternions(
    n: int, dtype: Optional[torch.dtype] = None, device: Optional[Device] = None
):
    """
    Generate random quaternions representing rotations,
    i.e. versors with nonnegative real part.

    Args:
        n: Number of quaternions in a batch to return.
        dtype: Type to return.
        device: Desired device of returned tensor. Default:
            uses the current device for the default tensor type.

    Returns:
        Quaternions as tensor of shape (N, 4).
    """
    o = torch.randn((n, 4), dtype=dtype, device=device)
    s = (o * o).sum(1)
    o = o / _copysign(torch.sqrt(s), o[:, 0])[:, None]
    return o


def random_rotations(
    n: int, dtype: Optional[torch.dtype] = None, device: Optional[Device] = None
):
    """
    Generate random rotations as 3x3 rotation matrices.

    Args:
        n: Number of rotation matrices in a batch to return.
        dtype: Type to return.
        device: Device of returned tensor. Default: if None,
            uses the current device for the default tensor type.

    Returns:
        Rotation matrices as tensor of shape (n, 3, 3).
    """
    quaternions = random_quaternions(n, dtype=dtype, device=device)
    return quaternion_to_matrix(quaternions)


def random_rotation(
    dtype: Optional[torch.dtype] = None, device: Optional[Device] = None
):
    """
    Generate a single random 3x3 rotation matrix.

    Args:
        dtype: Type to return
        device: Device of returned tensor. Default: if None,
            uses the current device for the default tensor type

    Returns:
        Rotation matrix as tensor of shape (3, 3).
    """
    return random_rotations(1, dtype, device)[0]


def standardize_quaternion(quaternions):
    """
    Convert a unit quaternion to a standard form: one in which the real
    part is non negative.

    Args:
        quaternions: Quaternions with real part first,
            as tensor of shape (..., 4).

    Returns:
        Standardized quaternions as tensor of shape (..., 4).
    """
    return torch.where(quaternions[..., 0:1] < 0, -quaternions, quaternions)


def quaternion_raw_multiply(a, b):
    """
    Multiply two quaternions.
    Usual torch rules for broadcasting apply.

    Args:
        a: Quaternions as tensor of shape (..., 4), real part first.
        b: Quaternions as tensor of shape (..., 4), real part first.

    Returns:
        The product of a and b, a tensor of quaternions shape (..., 4).
    """
    aw, ax, ay, az = torch.unbind(a, -1)
    bw, bx, by, bz = torch.unbind(b, -1)
    ow = aw * bw - ax * bx - ay * by - az * bz
    ox = aw * bx + ax * bw + ay * bz - az * by
    oy = aw * by - ax * bz + ay * bw + az * bx
    oz = aw * bz + ax * by - ay * bx + az * bw
    return torch.stack((ow, ox, oy, oz), -1)


def quaternion_multiply(a, b):
    """
    Multiply two quaternions representing rotations, returning the quaternion
    representing their composition, i.e. the versor with nonnegative real part.
    Usual torch rules for broadcasting apply.

    Args:
        a: Quaternions as tensor of shape (..., 4), real part first.
        b: Quaternions as tensor of shape (..., 4), real part first.

    Returns:
        The product of a and b, a tensor of quaternions of shape (..., 4).
    """
    ab = quaternion_raw_multiply(a, b)
    return standardize_quaternion(ab)


def quaternion_invert(quaternion):
    """
    Given a quaternion representing rotation, get the quaternion representing
    its inverse.

    Args:
        quaternion: Quaternions as tensor of shape (..., 4), with real part
            first, which must be versors (unit quaternions).

    Returns:
        The inverse, a tensor of quaternions of shape (..., 4).
    """

    return quaternion * quaternion.new_tensor([1, -1, -1, -1])


def quaternion_apply(quaternion, point):
    """
    Apply the rotation given by a quaternion to a 3D point.
    Usual torch rules for broadcasting apply.

    Args:
        quaternion: Tensor of quaternions, real part first, of shape (..., 4).
        point: Tensor of 3D points of shape (..., 3).

    Returns:
        Tensor of rotated points of shape (..., 3).
    """
    if point.size(-1) != 3:
        raise ValueError(f"Points are not in 3D, f{point.shape}.")
    real_parts = point.new_zeros(point.shape[:-1] + (1,))
    point_as_quaternion = torch.cat((real_parts, point), -1)
    out = quaternion_raw_multiply(
        quaternion_raw_multiply(quaternion, point_as_quaternion),
        quaternion_invert(quaternion),
    )
    return out[..., 1:]


def axis_angle_to_matrix(axis_angle):
    """
    Convert rotations given as axis/angle to rotation matrices.

    Args:
        axis_angle: Rotations given as a vector in axis angle form,
            as a tensor of shape (..., 3), where the magnitude is
            the angle turned anticlockwise in radians around the
            vector's direction.

    Returns:
        Rotation matrices as tensor of shape (..., 3, 3).
    """
    return quaternion_to_matrix(axis_angle_to_quaternion(axis_angle))


def matrix_to_axis_angle(matrix):
    """
    Convert rotations given as rotation matrices to axis/angle.

    Args:
        matrix: Rotation matrices as tensor of shape (..., 3, 3).

    Returns:
        Rotations given as a vector in axis angle form, as a tensor
            of shape (..., 3), where the magnitude is the angle
            turned anticlockwise in radians around the vector's
            direction.
    """
    return quaternion_to_axis_angle(matrix_to_quaternion(matrix))


def axis_angle_to_quaternion(axis_angle):
    """
    Convert rotations given as axis/angle to quaternions.

    Args:
        axis_angle: Rotations given as a vector in axis angle form,
            as a tensor of shape (..., 3), where the magnitude is
            the angle turned anticlockwise in radians around the
            vector's direction.

    Returns:
        quaternions with real part first, as tensor of shape (..., 4).
    """
    angles = torch.norm(axis_angle, p=2, dim=-1, keepdim=True)
    half_angles = 0.5 * angles
    eps = 1e-6
    small_angles = angles.abs() < eps
    sin_half_angles_over_angles = torch.empty_like(angles)
    sin_half_angles_over_angles[~small_angles] = (
        torch.sin(half_angles[~small_angles]) / angles[~small_angles]
    )
    # for x small, sin(x/2) is about x/2 - (x/2)^3/6
    # so sin(x/2)/x is about 1/2 - (x*x)/48
    sin_half_angles_over_angles[small_angles] = (
        0.5 - (angles[small_angles] * angles[small_angles]) / 48
    )
    quaternions = torch.cat(
        [torch.cos(half_angles), axis_angle * sin_half_angles_over_angles], dim=-1
    )
    return quaternions


def quaternion_to_axis_angle(quaternions):
    """
    Convert rotations given as quaternions to axis/angle.

    Args:
        quaternions: quaternions with real part first,
            as tensor of shape (..., 4).

    Returns:
        Rotations given as a vector in axis angle form, as a tensor
            of shape (..., 3), where the magnitude is the angle
            turned anticlockwise in radians around the vector's
            direction.
    """
    norms = torch.norm(quaternions[..., 1:], p=2, dim=-1, keepdim=True)
    half_angles = torch.atan2(norms, quaternions[..., :1])
    angles = 2 * half_angles
    eps = 1e-6
    small_angles = angles.abs() < eps
    sin_half_angles_over_angles = torch.empty_like(angles)
    sin_half_angles_over_angles[~small_angles] = (
        torch.sin(half_angles[~small_angles]) / angles[~small_angles]
    )
    # for x small, sin(x/2) is about x/2 - (x/2)^3/6
    # so sin(x/2)/x is about 1/2 - (x*x)/48
    sin_half_angles_over_angles[small_angles] = (
        0.5 - (angles[small_angles] * angles[small_angles]) / 48
    )
    return quaternions[..., 1:] / sin_half_angles_over_angles


def rotation_6d_to_matrix(d6: torch.Tensor) -> torch.Tensor:
    """
    Converts 6D rotation representation by Zhou et al. [1] to rotation matrix
    using Gram--Schmidt orthogonalization per Section B of [1].
    Args:
        d6: 6D rotation representation, of size (*, 6)

    Returns:
        batch of rotation matrices of size (*, 3, 3)

    [1] Zhou, Y., Barnes, C., Lu, J., Yang, J., & Li, H.
    On the Continuity of Rotation Representations in Neural Networks.
    IEEE Conference on Computer Vision and Pattern Recognition, 2019.
    Retrieved from http://arxiv.org/abs/1812.07035
    """

    a1, a2 = d6[..., :3], d6[..., 3:]
    b1 = F.normalize(a1, dim=-1)
    b2 = a2 - (b1 * a2).sum(-1, keepdim=True) * b1
    b2 = F.normalize(b2, dim=-1)
    b3 = torch.cross(b1, b2, dim=-1)
    return torch.stack((b1, b2, b3), dim=-2)


def matrix_to_rotation_6d(matrix: torch.Tensor) -> torch.Tensor:
    """
    Converts rotation matrices to 6D rotation representation by Zhou et al. [1]
    by dropping the last row. Note that 6D representation is not unique.
    Args:
        matrix: batch of rotation matrices of size (*, 3, 3)

    Returns:
        6D rotation representation, of size (*, 6)

    [1] Zhou, Y., Barnes, C., Lu, J., Yang, J., & Li, H.
    On the Continuity of Rotation Representations in Neural Networks.
    IEEE Conference on Computer Vision and Pattern Recognition, 2019.
    Retrieved from http://arxiv.org/abs/1812.07035
    """
    return matrix[..., :2, :].clone().reshape(*matrix.size()[:-2], 6)

Reference

[1] https://blog.csdn.net/weixin_43357695/article/details/126063091

[2]https://zhuanlan.zhihu.com/p/45404840

举报

相关推荐

react基本使用

学习笔记python

react hooks基本使用

react/react-nativereactJavaScr...让前端飞

react-redux的基本使用

react.jsreact-redux

【react-redux】的基本使用

react.jsjavascript前端

React 语法基本使用介绍

React基础前端

12 React路由基本的使用（一）

微信高亮显示javascript前端开发

reactjs react-redux的基本使用

react.js前端reactjs

React的基本介绍

插值复用htmlHtml/CSS前端开发yyds干货盘点

React 基本介绍

react.jsjavascript前端

好客租房3-React的基本使用

子节点JavaScript前端开发
0 条评论