深入了解Flutter中Overlay的介绍以及使用

1.单点修改+区间查询

P3374 【模板】树状数组 1

题目描述

如题，已知一个数列，你需要进行下面两种操作：

• 将某一个数加上 x

• 求出某区间每一个数的和

输入格式

第一行包含两个正整数 n,m，分别表示该数列数字的个数和操作的总个数。

第二行包含 n 个用空格分隔的整数，其中第 i 个数字表示数列第 i 项的初始值。

接下来 m 行每行包含 3 个整数，表示一个操作，具体如下：

• 1 x k 含义：将第 x 个数加上 k

• 2 x y 含义：输出区间 [x,y] 内每个数的和

输出格式

输出包含若干行整数，即为所有操作 22 的结果。

输入输出样例

输入 #1

5 5
1 5 4 2 3
1 1 3
2 2 5
1 3 -1
1 4 2
2 1 4

输出 #1

14
16

说明/提示

【数据范围】

对于 30% 的数据，1≤n≤8，1≤m≤10；
对于 70% 的数据，1≤n,m≤10^4；
对于 100% 的数据，1≤n,m≤5×10^5。

数据保证对于任意时刻，a 的任意子区间（包括长度为 1 和 n 的子区间）和均在 [−231,231) 范围内。

样例说明：

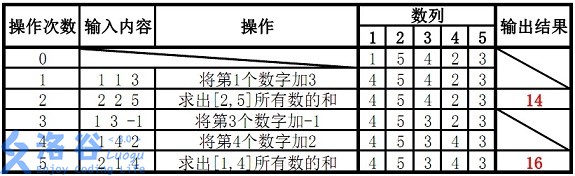
故输出结果14、16

解题思路

单点修改操作：递归到叶子结点，然后对叶子结点进行修改，然后返回的时候又改变其父节点

void find(int p, int x, int k)
{
	if (a[p].l == a[p].r)//到叶子结点，直接修改
	{
		a[p].data += k;
		return;
	}
	if (x <= a[2 * p].r)
		find(2 * p, x, k);
	else
		find(2 * p + 1, x, k);
	//回溯修改父类结点
	a[p].data = a[2 * p].data + a[2 * p + 1].data;
}

 区间查询：当递归调用的区间完全在查询的区间里面，直接返回对应的值,节约时间,当递归区间没有在查询的区间内直接返回0，当有部分区间在查询区间里面直接返回

int modify(int p, int l, int r)
{
	if (a[p].l >= l && a[p].r <= r) //完全在查询区间里面
	{
		return a[p].data;
	}
	if (a[p].r<l || a[p].l>r) //完全不在查询区间里面
		return 0;
	int an = 0;
	部分在查询区间里面
	if (l <= a[2 * p].r)
		an += modify(p * 2, l, r);
	if (r >= a[2 * p + 1].l)
		an += modify(p * 2 + 1, l, r);
	return an;
}

完整代码

#include<stdio.h>
int n, m;
struct nnn {
	int data;
	int l, r;
}a[2000010];
int b[500010], ans;
//建树
void dfs(int x,int l,int r)
{
	a[x].l = l; a[x].r = r;
	if (l == r)//叶子结点赋值
	{
		a[x].data = b[l];
		return;
	}
	int mid = (l + r) / 2;
	dfs(2 * x,l,mid);
	dfs(2 * x + 1, mid + 1, r);
	a[x].data = a[2 * x].data + a[2 * x + 1].data;
}
//区间查询
int modify(int p, int l, int r)
{
	if (a[p].l >= l && a[p].r <= r) //完全在查询区间里面
	{
		return a[p].data;
	}
	if (a[p].r<l || a[p].l>r) //完全不在查询区间里面
		return 0;
	int an = 0;
	部分在查询区间里面
	if (l <= a[2 * p].r)
		an += modify(p * 2, l, r);
	if (r >= a[2 * p + 1].l)
		an += modify(p * 2 + 1, l, r);
	return an;
}
//单点修改
void find(int p, int x, int k)
{
	if (a[p].l == a[p].r)//到叶子结点，直接修改
	{
		a[p].data += k;
		return;
	}
	if (x <= a[2 * p].r)
		find(2 * p, x, k);
	else
		find(2 * p + 1, x, k);
	//回溯修改父类结点
	a[p].data = a[2 * p].data + a[2 * p + 1].data;
}
int main()
{
	int c, u, v, k;
	scanf("%d %d", &n, &m);
	for (int i = 1; i <= n; i++)
		scanf("%d", &b[i]);
	dfs(1, 1, n);
	while (m--)
	{
		scanf("%d %d %d", &c, &v, &k);
		if (c == 1)
			find(1, v, k);
		else
		{
			ans = modify(1, v, k);
			printf("%d\n", ans);
		}
	}
	return 0;
}

2.区间修改+单点查询

P3368 【模板】树状数组 2

题目描述

如题，已知一个数列，你需要进行下面两种操作：

1. 将某区间每一个数加上 x；

2. 求出某一个数的值。

输入格式

第一行包含两个整数 N、M，分别表示该数列数字的个数和操作的总个数。

第二行包含 N 个用空格分隔的整数，其中第 i 个数字表示数列第 i 项的初始值。

接下来 M 行每行包含 2 或 4个整数，表示一个操作，具体如下：

操作 1： 格式：1 x y k 含义：将区间 [x,y] 内每个数加上 k；

操作 2： 格式：2 x 含义：输出第 x 个数的值。

输出格式

输出包含若干行整数，即为所有操作 22 的结果。

输入输出样例

输入 #1

5 5
1 5 4 2 3
1 2 4 2
2 3
1 1 5 -1
1 3 5 7
2 4

输出 #1

6
10

说明/提示

样例 1 解释：

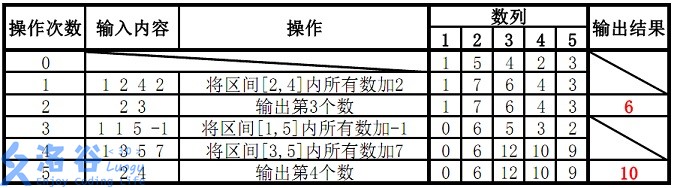
故输出结果为 6、10。

数据规模与约定

对于 30% 的数据：8N≤8，M≤10；

对于 70% 的数据：N≤10000，M≤10000；

对于 100% 的数据：1≤N,M≤500000，1≤x,y≤n，保证任意时刻序列中任意元素的绝对值都不大于 2^30。

解题思路

基本操作和上面一样，修改与查询改一下就可以了

完整代码

#include<stdio.h>
int n, m;
struct nnn {
	int data;
	int l, r;
}a[2000010];
int b[500010], ans;
//建树
void dfs(int x,int l,int r)
{
	a[x].l = l; a[x].r = r; a[x].data = 0;
	if (l == r)
	{
		a[x].data = b[l];
		return;
	}
	int mid = (l + r) / 2;
	dfs(2 * x,l,mid);
	dfs(2 * x + 1, mid + 1, r);
	//a[x].data = a[2 * x].data + a[2 * x + 1].data;
}
//区间修改
void modify(int p, int l, int r, int k)
{
	if (a[p].l >= l && a[p].r <= r) {
		a[p].data += k;
		return;
	}
	int mid = (a[p].l + a[p].r) /2 ;
	if (l <= mid)
		modify(p *2 , l, r, k);
	if (r > mid)
		modify(p *2 + 1, l, r, k);
}
//单点查询
void find(int p, int x)
{
	ans += a[p].data;
	if (a[p].l == a[p].r) return;
	int mid = (a[p].l + a[p].r) / 2;
	if (x <= mid)
		find(2 * p, x);
	else
		find(2 * p + 1, x);
}
int main()
{
	int c, u, v, k;
	scanf("%d %d", &n, &m);
	for (int i = 1; i <= n; i++)
		scanf("%d", &b[i]);
	dfs(1, 1, n);
	while (m--)
	{
		scanf("%d", &c);
		if (c == 1)
		{
			scanf("%d %d %d", &u, &v, &k);
			modify(1, u, v, k);
		}
		else
		{
			ans = 0;
			int d;
			scanf("%d", &d);
			find(1, d);
			printf("%d\n", ans);
		}
	}
	return 0;
}

3(区间修改+区间查询)

P3372 【模板】线段树 1

题目描述

如题，已知一个数列，你需要进行下面两种操作：

1. 将某区间每一个数加上 k。
2. 求出某区间每一个数的和。

输入格式

第一行包含两个整数 n,m，分别表示该数列数字的个数和操作的总个数。

第二行包含 n 个用空格分隔的整数，其中第 i 个数字表示数列第 i 项的初始值。

接下来 m 行每行包含 3 或 4 个整数，表示一个操作，具体如下：

1. 1 x y k：将区间 [x,y] 内每个数加上 k。
2. 2 x y：输出区间 [x,y] 内每个数的和。

输出格式

输出包含若干行整数，即为所有操作 2 的结果。

输入输出样例

输入 #1

5 5
1 5 4 2 3
2 2 4
1 2 3 2
2 3 4
1 1 5 1
2 1 4

输出 #1

11
8
20

说明/提示

对于 30% 的数据：n≤8，m≤10。
对于 70% 的数据：n≤10^3，m≤10^4。
对于 100% 的数据：1≤n,m≤10^5。

保证任意时刻数列中所有元素的绝对值之和 ≤1018≤1018。

【样例解释】

 解题思路

这里并不是把前面两种结合一下就可以了，需要用一个懒标记记录需要向下传多少给儿子

向下传的代码

void push_down(long long p)
{
	if (a[p].lz != 0)
	{
		a[p * 2].lz += a[p].lz;//左右儿子分别加上父亲的lz
		a[p * 2 + 1].lz += a[p].lz;
		long long mid = (a[p].l + a[p].r) / 2;
		a[2 * p].data += a[p].lz * (mid - a[2 * p].l + 1);
		a[2 * p + 1].data += a[p].lz * (a[2 * p + 1].r - mid);
		a[p].lz = 0;
	}
}

完整代码

#include<stdio.h>
long long n, m;
struct nnn {
	long long data;
	long long l, r, lz;
}a[2000010];
long long b[500010], ans;
//建树
void dfs(long long x, long long l, long long r)
{
	a[x].l = l; a[x].r = r;
	if (l == r)
	{
		a[x].data = b[l];
		return;
	}
	long long mid = (l + r) / 2;
	dfs(2 * x, l, mid);
	dfs(2 * x + 1, mid + 1, r);
	a[x].data = a[2 * x].data + a[2 * x + 1].data;
}
void push_down(long long p)
{
	if (a[p].lz != 0)
	{
		a[p * 2].lz += a[p].lz;//左右儿子分别加上父亲的lz
		a[p * 2 + 1].lz += a[p].lz;
		long long mid = (a[p].l + a[p].r) / 2;
		a[2 * p].data += a[p].lz * (mid - a[2 * p].l + 1);
		a[2 * p + 1].data += a[p].lz * (a[2 * p + 1].r - mid);
		a[p].lz = 0;
	}
}
void modify(long long p, long long l, long long r, long long k)
{
	if (a[p].l >= l && a[p].r <= r) {
		a[p].data += k * (a[p].r - a[p].l + 1);
		a[p].lz += k;
		return;
	}
	push_down(p);
	long long mid = (a[p].l + a[p].r) / 2;
	if (l <= mid)
		modify(p * 2, l, r, k);
	if (r > mid)
		modify(p * 2 + 1, l, r, k);
	a[p].data = a[p * 2].data + a[p * 2 + 1].data;
}
long long find(long long p, long long l, long long r)
{
	if (a[p].l >= l && a[p].r <= r) {
		return a[p].data;
	}
	if (a[p].r<l || a[p].l>r)
		return 0;
	push_down(p);
	long long an = 0;
	if (l <= a[2 * p].r)
		an += find(p * 2, l, r);
	if (r >= a[2 * p + 1].l)
		an += find(p * 2 + 1, l, r);
	return an;
}
int main()
{
	int c;
	long long u, v, k;
	scanf("%lld %lld", &n, &m);
	for (int i = 1; i <= n; i++)
		scanf("%lld", &b[i]);
	dfs(1, 1, n);
	while (m--)
	{
		scanf("%d", &c);
		if (c == 1)
		{
			scanf("%lld %lld %lld", &u, &v, &k);
			modify(1, u, v, k);
		}
		else
		{
			scanf("%lld %lld", &u, &v);
			ans = find(1, u, v);
			printf("%lld\n", ans);
		}
	}
	return 0;
}