目录
一、第一章——行列式
§1 二阶与三阶行列式
一、二元线性方程组与二阶行列式
书中由二元线性方程组引出二阶行列式,既讲述了行列式的一些基本语义概念也讲述了一种全新解二元线性方程组的方法.
 由上述例子引出概念
由上述例子引出概念

进而我们开启一个船新版本,线性代数。下面运用行列式解二元线性方程组.

以下方法也能得到正确结果,总之,注意系数的变化要对应。

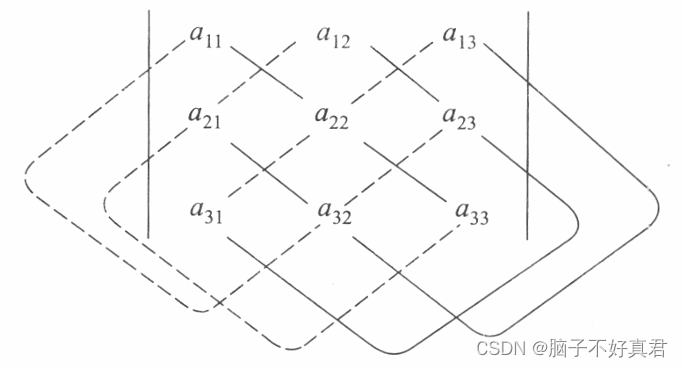
二、三阶行列式
计算三阶行列式的值,依旧运用对角线法则.
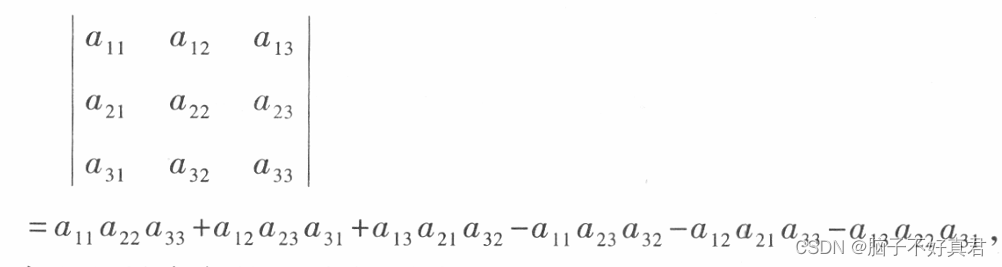
§2 全排列和对换
一、排列及其逆序数
1. 全排列:把n个不同的元素排成一列,叫做这n个元素的全排列(也简称排列).
2. 逆序数:一个排列中所有逆序的总数叫做这个排列的逆序数.
3. 奇排序:逆序数为奇数的排列叫做奇排列。偶排序:逆序数为偶数的排列叫做偶排列.
举例来说,n个元素如果一个标准次序排列,并且这n个元素正是按这个标准次序排列的,那么这个排列的逆序数等于0;当某一个元素不符合标准次序时,比如1、2、3、4、5这五个元素的标准次序排列是从小到大,如果这五个元素2,3,4,5,1如此排列,对于2,2前面没有比2大的数,设逆序数为t0,则t0=0;对于3,3前面的2比3小,不违反标准次序,设逆序数为t2,则t2=0;依此类推,对于4、5,t3=0,t4=0,但对于1,1前面的四个数都比1大,违反标准次序,所以t5=4。最终总逆序数t=t1+t2+t3+t4+t5=4,4是偶数,所以这个排列叫做偶排列.

二、对换
1. 在排列中,将任意两个元素对调,其余的元素不动,这种作出新排列的手续叫做对换。将相邻两个元素对换,叫做相邻对换.
2. 定理1 一个排列中的任意两个元素对换,排列改变奇偶性.
3. 推论 奇排列对换成标准排列的对换次数为奇数,偶排列对换成标准排列的对换次数 为偶数.
§3 n阶行列式的定义

由三阶行列式可以类推出,n阶行列式如下:
其中 p1 p2...pn 为自然数1 ,2,…,n的一个排列,t为这个排列的逆序数.由于这样的排列共有n!个,因而a1p1 a2p2 ... anpn 的项共有n!项.所有这n!项的代数和 ∑(-1 )^t *a1p1*a2p2 … anp n 称为n阶行列式. 记作D=|...|,简记作det(aij).
上三角行列式、下三角行列式、对角行列式如下:
§4 行列式的性质
转置行列式,行作列,列作行.
性质1 行列式与它的转置行列式相等. 
性质2 对换行列式的两行(列),行列式变号. 
推论 如果行列式有两行(列)完全相同,则此行列式等于零. 
性质3 行列式的某一行(列)中所有的元素都乘同一数 k,等于用数 k 乘此行列式. 
推论 行列式中某一行(列)的所有元素的公因子可以提到行列式记号的外面.
证明 同性质3
性质4 行列式中如果有两行(列)元素成比例,则此行列式等于零.
性质5 若行列式的某一行(列)的元素都是两数之和,例如第 i 行的元素都是两数之和,则D等于下列两个行列式之和.
性质6 把行列式的某一行(列)的各元素乘同一数然后加到另一行(列)对应的元素上去,行列式不变.









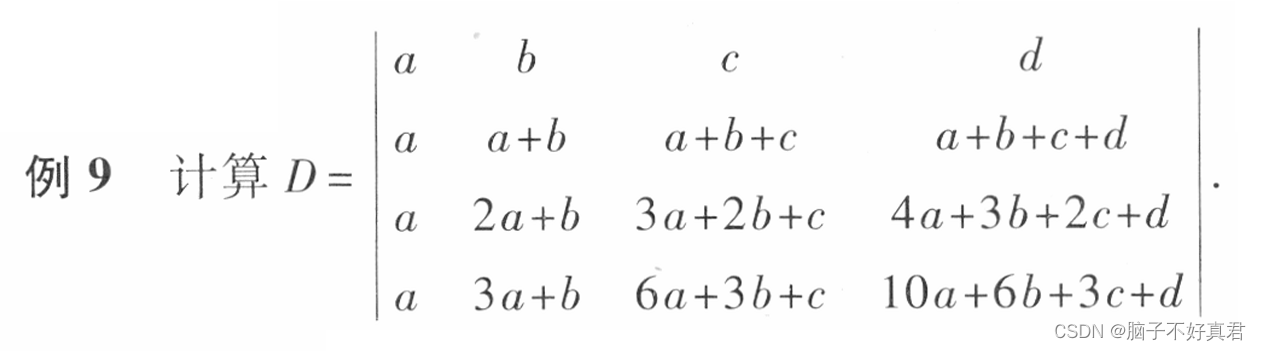
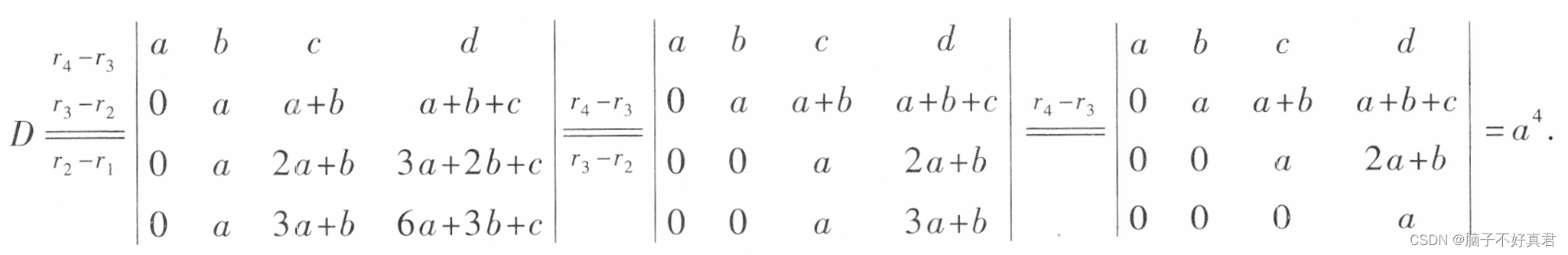
例10、例11直接看不懂 


§5 行列式按行(列)展开
1. 余子式
在n阶行列式中,把(i,j)元 aij 所在的第i行和第j列划去后,留下来的 n-1 阶行列式叫做(i,j)元 aij 的余子式,记作 Mij.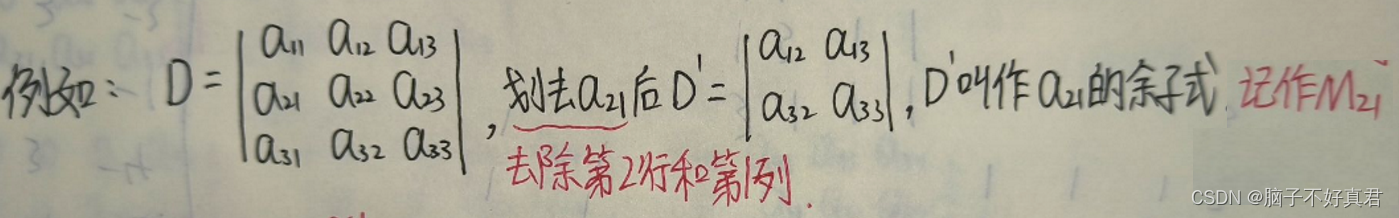
2. 代数余子式
记Aij = (-1)^i+j * Mij,Aij 叫做(i,j)元 aij 的代数余子式.
引理 一个n阶行列式,如果其中第i行所有元素除(i,j)元 aij 外都为零,那么这行列式等于 ai j与它的代数余子式的乘积,即D = aij * Aij.
定理2 行列式等于它的任一行(列)的各元素与其对应的代数余子式乘积 之和,即
D =ai1Ai1 + ai2Ai2 + … + ainAin (i=1,2,…,n)
D =a1jA1j + a2jA2j + … + anjAnj (j=1 ,2,… ,n)
由性质5可证
这个定理叫做行列式按行(列)展开法则.利用这一法则并结合行列式的性质,可以简化行列式的计算.






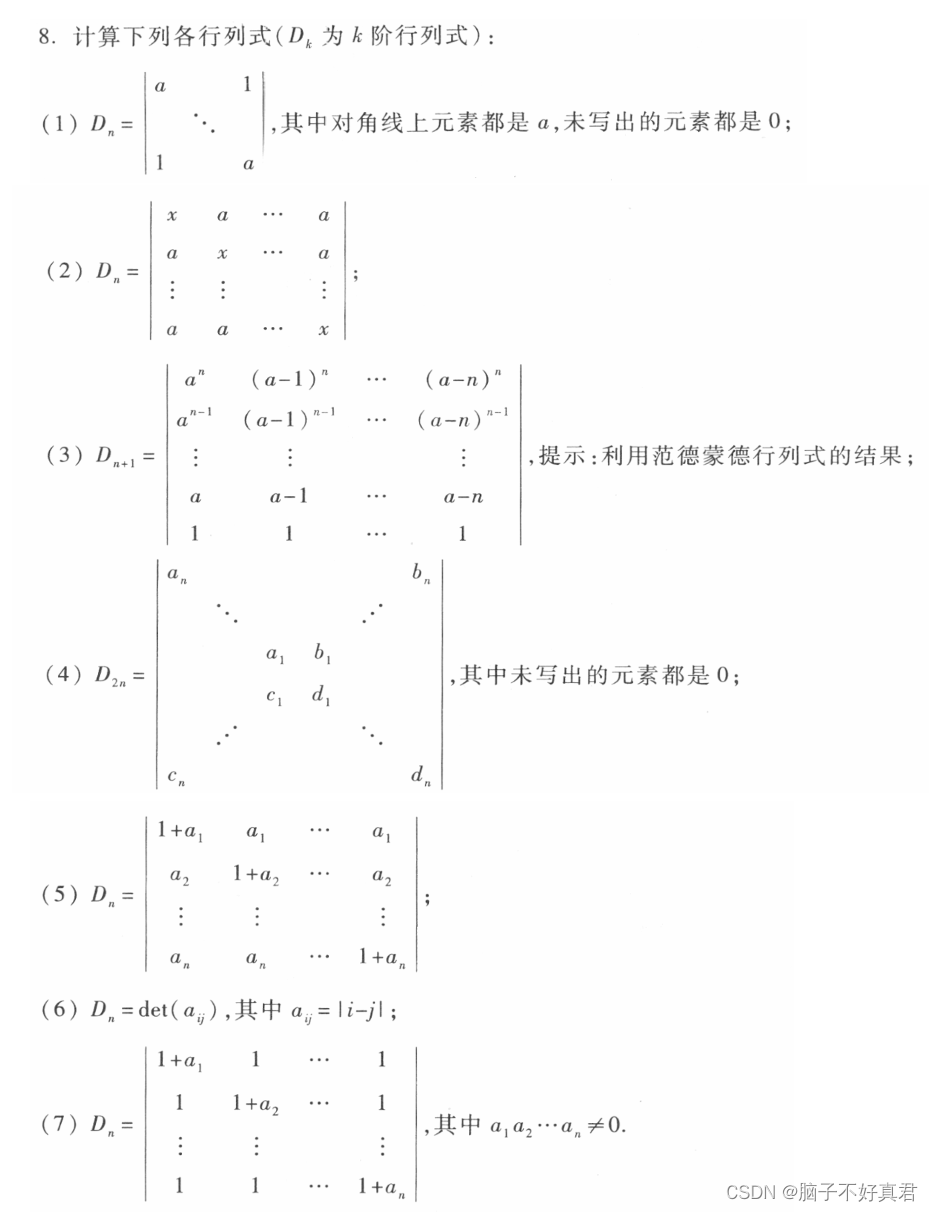
二、习题一
每一项的元素必须来自行列式的不同行和不同列,这是由于行列式的定义和性质决定的。
行列式是一个数学工具,表示了一个等阶矩阵经过线性变换后的伸缩因子,你可以理解为空间的“体积”。为了保证线性独立,我们在计算行列式时,必须使用每一行和每一列的元素。从每一行和每一列选择一个元素(且选择的元素不在同一行或同一列)来构成一项,保证了我们能全面地反映出所有线性基向量的变化。
如果行列式中有两个元素在同一行或同一列,那么这两个变量就会失去线性独立性,会增加问题的复杂性。因此,为了保证准确性和简单性,我们必须让行列式中的每一项都由不同行和不同列的元素构成。
从更深层次理解,当我们选择相同行或列的两个元素时,我们实际上是在计算某个空间中的两个平行线段的有向体积,这显然结果应为0。因此,我们必须从不同行列选择元素,才能有效地描述空间变换的“体积”变化。
所以,因子a11和a23在行列式的每一个项中都必须配对两个其他地方的元素,而这两个元素必须来自剩下的行与列。


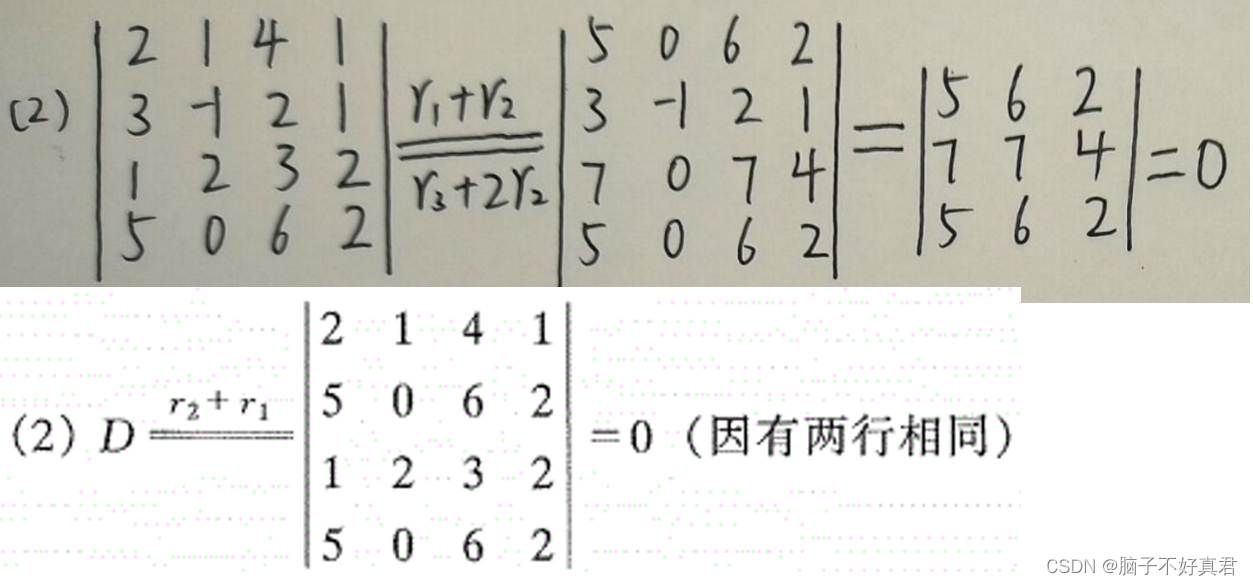







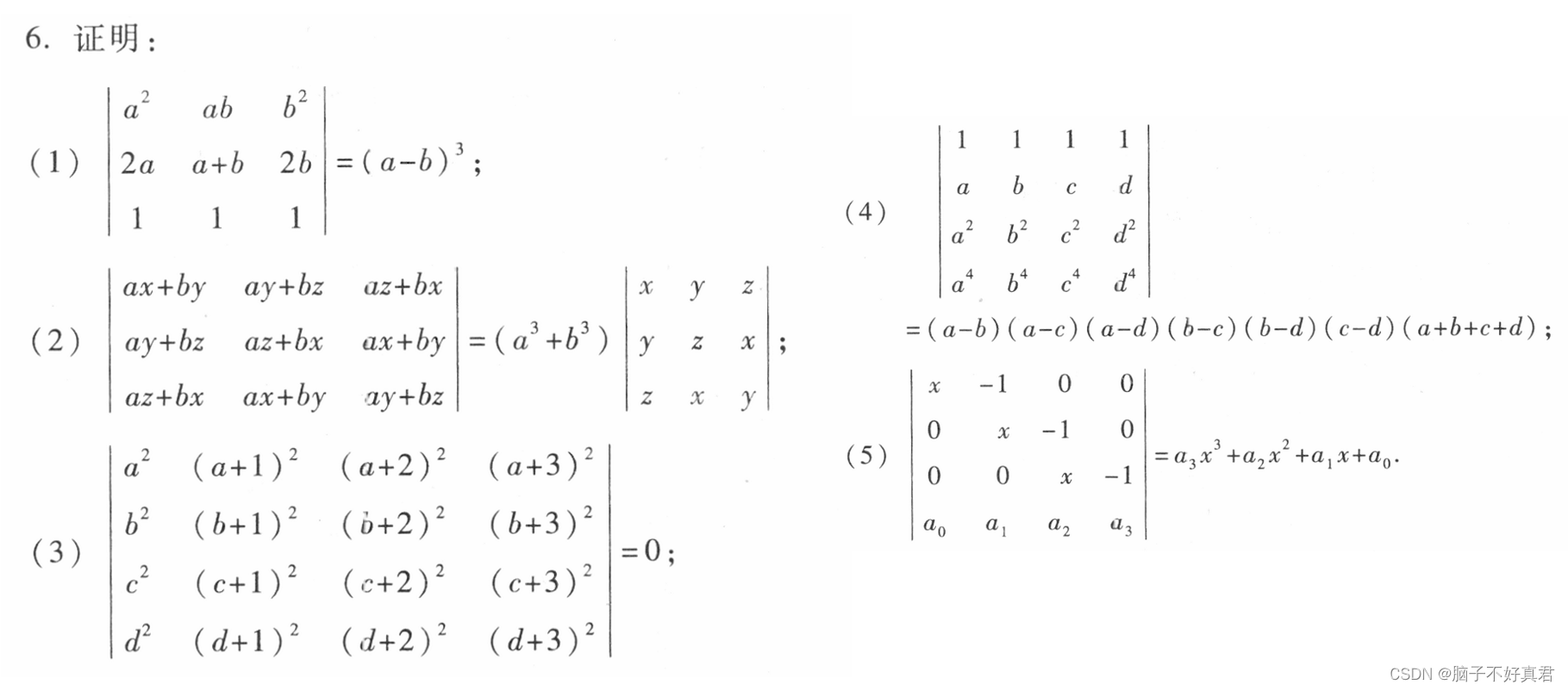
























三、参考书目
同济大学数学系. 工程数学 线性代数 第六版. 高等教育出版社. 2014
同济大学数学系. 线性代数 附册学习辅导与习题全解同济 第六版. 高等教育出版社. 2014
















