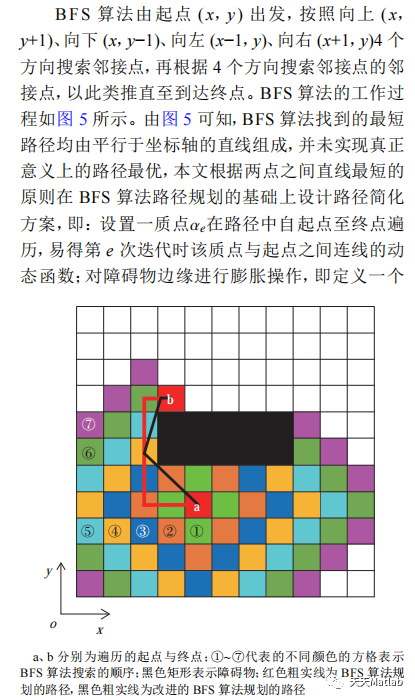
1 简介

2 部分代码

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%
% This function takes Obstacle edge coordinates, Workspace dimentions and
% generates a arena (Work Space) that is pre-processed for the allowed 
% Coordinates. For each point in the Work Space dimentions, it checks 
% wether it lies in Obstacle Space or in the Work Space.
% 
% The obstacle space is determined using Half plane Method. 
% We define equation of lines of each obstacle and use inequality to find
% weather the query point satiesfies all the inequalities or not. If it
% does then it lies inside or on the boundary of obstacle. If it is inside
% or on obstacle, it will be assigned a value of 1, otherwise 0. 
%  The result of this function is a Pre-Processed Work Space.
% 
% Then the main Program will expland only the nodes with value 0.
%
% Code By: Mayank Pathak
%     
%%%%
function [Arena] = ObstacleSpace_generator(Orectangle,Opolygon,Ocircle,Arena)
for i = 1:size(Arena,1)        % iterate about x axis
    for j = 1:size(Arena,2)    % iterate about y axis
        q_x = j;
        q_y = i;
%   Implementing inequality for rectangle
        if (ge(q_x,Orectangle(1,1)) && le(q_x,Orectangle(1,3)) &&...
           ge(q_y,Orectangle(2,1)) && le(q_y,Orectangle(2,3)))
             Arena(i,j) = 1;
%   Implementing inequality for Circle
        elseif le(sqrt((q_x-Ocircle(1))^2 + (q_y-Ocircle(2))^2),15)
             Arena(i,j) = 1;
        end
%   Implementing inequality for polygon
        [In,On] = inpolygon(q_x,q_y,Opolygon(1,:),Opolygon(2,:));
        if In || On
            Arena(i,j) = 1;
        end
    end
end
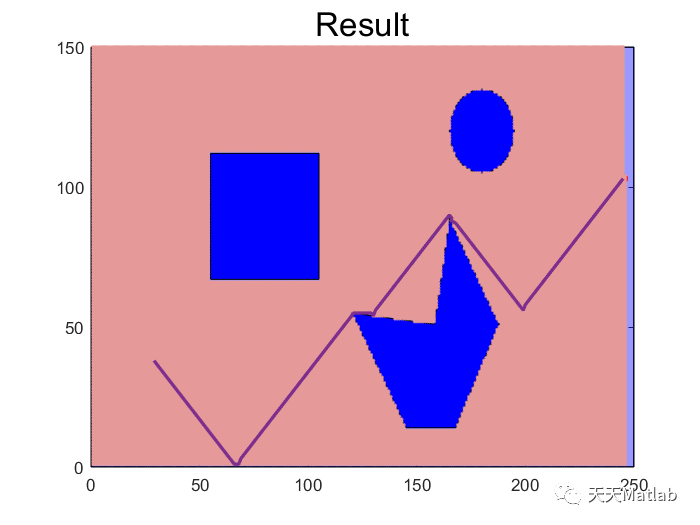
end

3 仿真结果

4 参考文献

[1]金何. 基于BFS算法的三维动态环境下机器人路径规划[D]. 河南大学.

博主简介：擅长智能优化算法、神经网络预测、信号处理、元胞自动机、图像处理、路径规划、无人机等多种领域的Matlab仿真，相关matlab代码问题可私信交流。

部分理论引用网络文献，若有侵权联系博主删除。