leetcode之杨辉三角
2022/3/31
(题源力扣)
题目简述:
给定一个非负整数 numRows,生成「杨辉三角」的前 numRows 行。
在「杨辉三角」中,每个数是它左上方和右上方的数的和。
示例 1:
输入: numRows = 5
输出: [[1],[1,1],[1,2,1],[1,3,3,1],[1,4,6,4,1]]
示例 2:
输入: numRows = 1
输出: [[1]]
提示:
1 <= numRows <= 30
还是python用的顺手啊(赞赏),,,(bushi
言归正传
如果只看题目原图
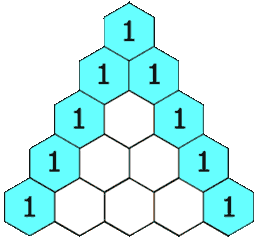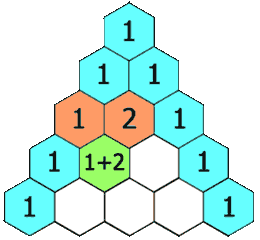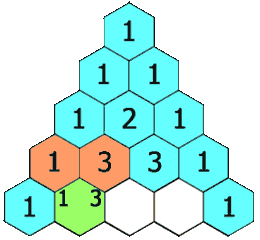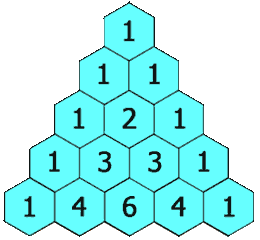
几乎不会让人有什么头绪,,
所以我们可以考虑到把杨辉三角写成类似下面这样的下三角形式,,
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
......
这个时候,我们就可以把杨辉三角的结构放到一个 n ∗ n n * n n∗n的矩阵(实际只用下三角区域,可以用遍历控制)中,并且很容易能总结出递推公式:
a j k = a j − 1 , k − 1 + a j − 1 , k a_{jk} = a_{j-1,k-1} + a_{j-1,k} ajk=aj−1,k−1+aj−1,k
式子中,
a
j
k
a_{jk}
ajk表示位于第j行第k列的元素。
要注意的是,这个公式需要
a
j
−
1
,
k
−
1
a_{j-1,k-1}
aj−1,k−1以及
a
j
−
1
,
k
a_{j-1,k}
aj−1,k存在,即只在某个元素位于第一列及对角线以外的位置适用。
实际上,通过进一步观察,我们可以发现, a i i a_{ii} aii(对角线元素)以及 a m 1 a_{m1} am1(第一列的元素)都是1,正好对应了上文公式不适用的情况。
python代码如下:
class Solution(object):
def generate(self, numRows):
"""
:type numRows: int
:rtype: List[List[int]]
"""
res = [] # 输出的矩阵
for i in range(numRows):
res.append([]) # 添加行维度
for j in range(numRows):
for k in range(j+1): # 注意范围,只要下三角,防止赋值次数错误
# 边缘元素赋值
if k == 0:
res[j].append(1) # 第一列元素
elif k == j:
res[j].append(1) # 对角线元素
else:
res[j].append(res[j-1][k-1] + res[j-1][k]) # 中间元素递推公式
k += 1
return res










