【Quarto】Markdown导出PPT-CFANZ编程社区

原题链接：2581. 统计可能的树根数目

题目描述：

Alice 有一棵 n 个节点的树，节点编号为 0 到 n - 1 。树用一个长度为 n - 1 的二维整数数组 edges 表示，其中 edges[i] = [ai, bi] ，表示树中节点 ai 和 bi 之间有一条边。

Alice 想要 Bob 找到这棵树的根。她允许 Bob 对这棵树进行若干次猜测。每一次猜测，Bob 做如下事情：

选择两个 不相等 的整数 u 和 v ，且树中必须存在边 [u, v] 。
Bob 猜测树中 u 是 v 的 父节点 。

Bob 的猜测用二维整数数组 guesses 表示，其中 guesses[j] = [uj, vj] 表示 Bob 猜 uj 是 vj 的父节点。

Alice 非常懒，她不想逐个回答 Bob 的猜测，只告诉 Bob 这些猜测里面至少有 k 个猜测的结果为 true 。

给你二维整数数组 edges ，Bob 的所有猜测和整数 k ，请你返回可能成为树根的 节点数目 。如果没有这样的树，则返回 0。

输入输出描述：

示例 1：

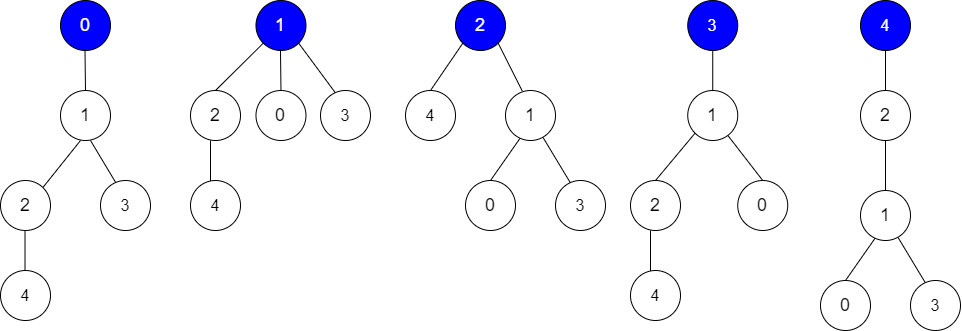
输入：edges = [[0,1],[1,2],[1,3],[4,2]], guesses = [[1,3],[0,1],[1,0],[2,4]], k = 3
输出：3
解释：
根为节点 0 ，正确的猜测为 [1,3], [0,1], [2,4]
根为节点 1 ，正确的猜测为 [1,3], [1,0], [2,4]
根为节点 2 ，正确的猜测为 [1,3], [1,0], [2,4]
根为节点 3 ，正确的猜测为 [1,0], [2,4]
根为节点 4 ，正确的猜测为 [1,3], [1,0]
节点 0 ，1 或 2 为根时，可以得到 3 个正确的猜测。

示例 2：

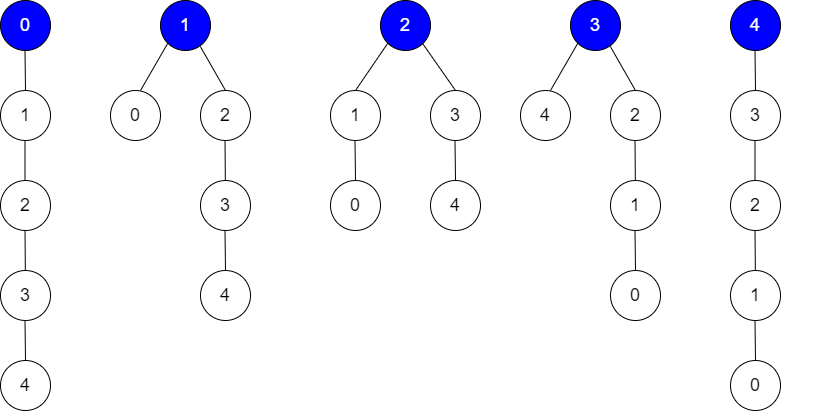
输入：edges = [[0,1],[1,2],[2,3],[3,4]], guesses = [[1,0],[3,4],[2,1],[3,2]], k = 1
输出：5
解释：
根为节点 0 ，正确的猜测为 [3,4]
根为节点 1 ，正确的猜测为 [1,0], [3,4]
根为节点 2 ，正确的猜测为 [1,0], [2,1], [3,4]
根为节点 3 ，正确的猜测为 [1,0], [2,1], [3,2], [3,4]
根为节点 4 ，正确的猜测为 [1,0], [2,1], [3,2]
任何节点为根，都至少有 1 个正确的猜测。

提示：

edges.length == n - 1
2 <= n <= 10^5
1 <= guesses.length <= 10^5
0 <= ai, bi, uj, vj <= n - 1
ai != bi
uj != vj
edges 表示一棵有效的树。
guesses[j] 是树中的一条边。
guesses 是唯一的。
0 <= k <= guesses.length

`解题思路：`

cpp代码如下:

class Solution {
public:
    int rootCount(vector<vector<int>>& edges, vector<vector<int>>& guesses, int k) {
        int ans=0,n=edges.size()+1;
        vector<vector<int>>g(n,vector<int>());
        for(auto& t:edges){   //邻接表建图
            int x=t[0],y=t[1];
            g[x].push_back(y);
            g[y].push_back(x);
        }

        map<pair<int,int>,int>mp;  //首先把所有的猜测存起来，用于后续判断
        for(auto& t:guesses){
            int x=t[0],y=t[1];
            mp[pair{x,y}]++;
        }

        function<int(int,int)>dfs1=[&](int x,int fa)->int {
            int res=0;
            for(auto& y:g[x]){
                if(y==fa)continue;
                if(mp.count(pair{x,y})){
                    res++;
                }
                res+=dfs1(y,x);
            }
            return res;
        };
        //首先考虑0号结点为根结点时，会有多少个猜测满足要求，用cnt记录
        int cnt=dfs1(0,-1);
        if(cnt>=k)ans++;  //这种情况如果满足要求，更新答案

        function<void(int,int,int)>dfs2=[&](int x,int fa,int cnt){
            for(auto& y:g[x]){
                if(y==fa)continue;
                int val=cnt;  //每个子树都是基于cnt进行的，所以先用一个val存起来
                //换根相当于把x->y的边变为y->x的边，其他的边不变
                if(mp.count(pair{x,y})){  //把x->y的边减去
                    val--;
                }
                if(mp.count(pair{y,x})){
                    val++;   //把y->x的加上
                }

                if(val>=k)ans++;   //更新答案
                dfs2(y,x,val);
            }
        };

        //然后考虑换根操作
        dfs2(0,-1,cnt);
        return ans;
    }
};