59.螺旋矩阵
59. 螺旋矩阵 II
labuladong 题解
给你一个正整数 n ,生成一个包含 1 到 n2 所有元素,且元素按顺时针顺序螺旋排列的 n x n 正方形矩阵 matrix 。
示例 1:
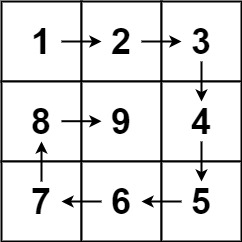
输入:n = 3 输出:[[1,2,3],[8,9,4],[7,6,5]]
示例 2:
输入:n = 1 输出:[[1]]
提示:
-
1 <= n <= 20
思路
-
由于是顺时针输入数据,我们可以把一个3*3的表格看作是三层甜甜圈,我们通过两次扒皮,和一次对n为奇数的单独赋值来实现我们顺时针输入数据的目的
-
由于我们要在循环里面完成这个任务,所以我们得让每一轮的规则都统一且恰当,比如说3*3的小格子,第一轮上下左右各填充2个数据就可以做到每次循环作用相同且和谐,当我们第一轮结束的时候,我们要奔赴第二个任务,开启对第二轮甜甜圈的征战,所以,我们要从当前的结束位置跳跃?为什么呢-->因为,我们在第一个元素的下面一个位置结束我们的循环,但是我们第二轮循环的开始是在我们第二行第二列,所以我们要重新定位起点坐标。
-
那怎么样才能做到呢?
-
为了做到这一点,我们引入两个变量,startx和starty,并规定每轮结束这两个变量的值都要加一来表示我们的起始位置改变,并且我们循环的第一句话就是让我们的循环变量来等于我们的x,y来方便我们进行操作
-
规定了起始位置只完成了任务的一半!别忘了,为了让我们的循环相同且恰当,我们还要要求每个循环不能乱写,必须要添加相同数量的值,所以我们引入偏移量offset,并把它初始化为1
-
我们的循环从startx开始,到startx+n-offset-1结束,为什么要加上startx呢?是因为我们要添加的数据总长度是n-offset,由于我们从startx开始,所以结尾也要加上startx.
-
每轮循环后,由于我们的新的循环较原来的循环来说,左右两边都少了一个数字,所以我们的offset要加2,如此往复,直到loop = 0;
-
还要注意,如果我们的n是奇数的话,那么我们循环过后中间的值并没有被赋上,我们需要单独给最中间的数字赋值
代码如下
class Solution {
public int[][] generateMatrix(int n) {
int[][] ans = new int[n][n];
int j,i;
int count = 1;
int loop = n/2;
int offset = 1;
int startx = 0;
int starty = 0;
while(loop>0)
{
i = startx;
j = starty;
for(;j<starty+n-offset;j++)
{
ans[i][j] = count;
count++;
}
for(;i<startx+n-offset;i++)
{
ans[i][j] = count;
count++;
}
for(;j>starty;j--)
{
ans[i][j] = count;
count++;
}
for(;i>startx;i--)
{
ans[i][j] = count;
count++;
}
loop--;
offset +=2;
startx++;
starty++;
}
if(n%2==1)
{
int mid = n/2;
ans[mid][mid] = count;
}
return ans;
}
}










