波动数组

观察这个数列：

1 3 0 2 -1 1 -2 …

这个数列中后一项总是比前一项增加2或者减少3，且每一项都为整数。

栋栋对这种数列很好奇，他想知道长度为 n 和为 s 而且后一项总是比前一项增加 a 或者减少 b 的整数数列可能有多少种呢？

输入格式

共一行，包含四个整数 n,s,a,bn,s,a,b，含义如前面所述。

输出格式

共一行，包含一个整数，表示满足条件的方案数。

由于这个数很大，请输出方案数除以 100000007 的余数。

数据范围

1≤n≤1000
−10^9≤s≤109,
1≤a,b≤10^6

输入样例：

4 10 2 3

输出样例：

样例解释

两个满足条件的数列分别是2 4 1 3和7 4 1 -2。

解

某次比赛不自量力的我被这道题折磨了。

分析思路：

在这里插入图片描述

#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

const int N = 1010, MOD = 100000007;

int f[N][N];

int get_mod(int a, int b)   // 求a除以b的正余数
{
    return (a % b + b) % b;
}

int main()
{
    int n, s, a, b;
    cin >> n >> s >> a >> b;

    f[0][0] = 1;
    for (int i = 1; i < n; i ++ )
        for (int j = 0; j < n; j ++ )
            f[i][j] = (f[i - 1][get_mod(j - a * (n - i), n)] + f[i - 1][get_mod(j + b * (n - i), n)]) % MOD;
    //如果从1开始则就是a*i;
    cout << f[n - 1][get_mod(s, n)] << endl;

    return 0;
}

二进制矩阵中的最短路径

给你一个 n x n 的二进制矩阵 grid 中，返回矩阵中最短 畅通路径 的长度。如果不存在这样的路径，返回 -1 。

二进制矩阵中的畅通路径是一条从 左上角 单元格（即，(0, 0)）到右下角单元格（即，(n - 1, n - 1)）的路径，该路径同时满足下述要求：

路径途经的所有单元格都的值都是 0 。
路径中所有相邻的单元格应当在 8 个方向之一 上连通（即，相邻两单元之间彼此不同且共享一条边或者一个角）。

畅通路径的长度 是该路径途经的单元格总数。

示例 1：

输入：grid = [[0,1],[1,0]]
输出：2

示例 2：

输入：grid = [[0,0,0],[1,1,0],[1,1,0]]
输出：4

示例 3：

输入：grid = [[1,0,0],[1,1,0],[1,1,0]]
输出：-1

提示：

n == grid.length
n == grid[i].length
1 <= n <= 100
grid[i][j] 为 0 或 1

解

这道题bfs练手题，注意斜线走算一步

class Solution {
public:
    const int dire[8][2]={{1,0},{-1,0},{0,1},{0,-1},{1,1},{1,-1},{-1,-1},{-1,1}};
    typedef pair<int, int> PII;
    int shortestPathBinaryMatrix(vector<vector<int>>& grid) {
        if( grid[0][0] == 1) return -1;
        int n = grid.size();
        int ans = 1;

        queue<PII> q;
        q.emplace(0,0);         //从0,0开始
        grid[0][0] = 1;
        while(!q.empty())
        {
            int m = q.size();
            while(m -- )
            {
                // PII u = q.front();
                auto [x,y]=q.front();
                q.pop();
                if(x == n-1 && y == n-1)
                    return ans;
                for(int i = 0;i < 8;i ++)//8个方向
                {
                    int dx = x + dire[i][0];
                    int dy = y + dire[i][1];
                    if(dx<0||dy<0||dx>=n||dy>=n) 
                        continue; 
                    if(grid[dx][dy]==0){        //判断是否能走
                        // q.emplace(dx,dy);
                        q.push({dx,dy});
                        grid[dx][dy]=1;         //标记
                    }
                }
            }
            ans++;
        }
        return -1;
    }
};

被围绕的区域

给你一个 m x n 的矩阵 board ，由若干字符 'X' 和 'O' ，找到所有被 'X' 围绕的区域，并将这些区域里所有的 'O' 用 'X' 填充。

示例 1：

输入：board = [["X","X","X","X"],["X","O","O","X"],["X","X","O","X"],["X","O","X","X"]]
输出：[["X","X","X","X"],["X","X","X","X"],["X","X","X","X"],["X","O","X","X"]]
解释：被围绕的区间不会存在于边界上，换句话说，任何边界上的 'O' 都不会被填充为 'X'。 任何不在边界上，或不与边界上的 'O' 相连的 'O' 最终都会被填充为 'X'。如果两个元素在水平或垂直方向相邻，则称它们是“相连”的。

示例 2：

输入：board = [["X"]]
输出：[["X"]]

提示：

m == board.length
n == board[i].length
1 <= m, n <= 200
board[i][j] 为 'X' 或 'O'

解

最开始把这道题想简单了，后面发现其实只需要判断四周的位置是不是O并且该位置是与否有相连的O就行

class Solution {
public:
    int n, m;
    void dfs(vector<vector<char>>& board, int x, int y) {
        //如果边上有O则只需要判断它周围是否有o就行
        //相当于找到的这个O就是没有被包围的
        if (x < 0 || x >= n || y < 0 || y >= m || board[x][y] != 'O') {
            return;
        }
        board[x][y] = 'A';
        dfs(board, x + 1, y);
        dfs(board, x - 1, y);
        dfs(board, x, y + 1);
        dfs(board, x, y - 1);
    }
    void solve(vector<vector<char>>& board) {
        n = board.size();

        if (n == 0) return;

        m = board[0].size();
        //四周的o变为a做标记
        for (int i = 0; i < n; i++) {
            dfs(board, i, 0);
            dfs(board, i, m - 1);
        }
        for (int i = 1; i < m - 1; i++) {
            dfs(board, 0, i);
            dfs(board, n - 1, i);
        }

        for (int i = 0; i < n; i++) {
            for (int j = 0; j < m; j++) {
                if (board[i][j] == 'A') {
                    board[i][j] = 'O';
                } else if (board[i][j] == 'O') {
                    board[i][j] = 'X';
                }
            }
        }
    }
};

所有可能的路径

给你一个有 n 个节点的 有向无环图（DAG），请你找出所有从节点 0 到节点 n-1 的路径并输出（不要求按特定顺序）

graph[i] 是一个从节点 i 可以访问的所有节点的列表（即从节点 i 到节点 graph[i][j]存在一条有向边）。

示例 1：

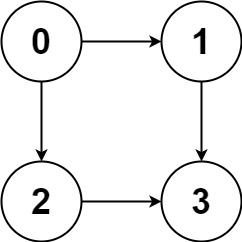
输入：graph = [[1,2],[3],[3],[]]
输出：[[0,1,3],[0,2,3]]
解释：有两条路径 0 -> 1 -> 3 和 0 -> 2 -> 3

示例 2：

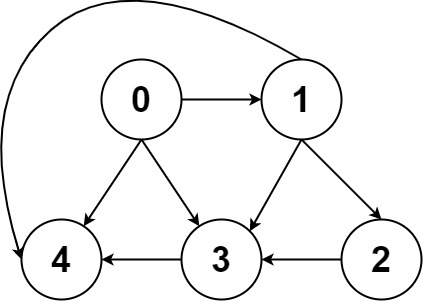
输入：graph = [[4,3,1],[3,2,4],[3],[4],[]]
输出：[[0,4],[0,3,4],[0,1,3,4],[0,1,2,3,4],[0,1,4]]

提示：

n == graph.length
2 <= n <= 15
0 <= graph[i][j] < n
graph[i][j] != i（即不存在自环）
graph[i] 中的所有元素 互不相同
保证输入为 有向无环图（DAG）

解

突然发现vector是真的牛逼

class Solution {
public:
    vector<vector<int>> ans;
    vector<int> st;

    void dfs(vector<vector<int>>& graph, int x, int n) {
        if (x == n) {
            ans.push_back(s);
            return;
        }
        for (auto& y : graph[x]) {
            st.push_back(y);
            dfs(graph, y, n);
            st.pop_back();
        }
    }
    vector<vector<int>> allPathsSourceTarget(vector<vector<int>>& graph) {
        stk.push_back(0);
        dfs(graph, 0, graph.size() - 1);
        return ans;
    }
};