Vue3判断变量和对象不为null和undefined-CFANZ编程社区

一、题目描述

给定两个整数数组 inorder 和 postorder ，其中 inorder 是二叉树的中序遍历， postorder 是同一棵树的后序遍历，请你构造并返回这颗 二叉树 。

示例 1:

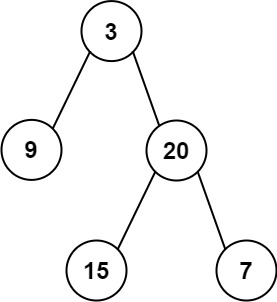
输入：inorder = [9,3,15,20,7], postorder = [9,15,7,20,3]
输出：[3,9,20,null,null,15,7]

示例 2:

输入：inorder = [-1], postorder = [-1]
输出：[-1]

提示:

1 <= inorder.length <= 3000
postorder.length == inorder.length
-3000 <= inorder[i], postorder[i] <= 3000
inorder 和 postorder 都由不同的值组成
postorder 中每一个值都在 inorder 中
inorder 保证是树的中序遍历
postorder 保证是树的后序遍历

二、解题思路

后序遍历的最后一个元素是树的根节点。
在中序遍历中找到根节点的位置，可以将中序遍历分成左右两个子树。
根据中序遍历中左右子树的长度，可以将后序遍历也分成左右两个子树。
递归地对左右子树进行上述步骤，构建出整棵树。

三、具体代码

class Solution {
    private Map<Integer, Integer> indexMap;

    public TreeNode buildTree(int[] inorder, int[] postorder) {
        indexMap = new HashMap<>();
        for (int i = 0; i < inorder.length; i++) {
            indexMap.put(inorder[i], i);
        }
        return buildTree(postorder, 0, postorder.length - 1, inorder, 0, inorder.length - 1);
    }

    private TreeNode buildTree(int[] postorder, int postStart, int postEnd, int[] inorder, int inStart, int inEnd) {
        if (postStart > postEnd || inStart > inEnd) {
            return null;
        }

        int rootVal = postorder[postEnd];
        TreeNode root = new TreeNode(rootVal);
        int index = indexMap.get(rootVal);

        int leftSize = index - inStart;
        int rightSize = inEnd - index;

        root.left = buildTree(postorder, postStart, postStart + leftSize - 1, inorder, inStart, index - 1);
        root.right = buildTree(postorder, postStart + leftSize, postEnd - 1, inorder, index + 1, inEnd);

        return root;
    }
}

四、时间复杂度和空间复杂度

1. 时间复杂度

构建索引映射表 indexMap 需要 O(n) 的时间，其中 n 是中序遍历的长度。
递归函数 buildTree 对于每个节点都会被调用一次，每次调用都会处理一个子树，子树的规模随层数减小而减小。在最坏的情况下，每次递归都会将问题规模减半，因此递归的深度为 O(log n)，但由于每次递归都需要进行一些常数时间的操作，所以每次递归的时间复杂度为 O(1)。因此，整个递归过程的时间复杂度为 O(n)。
综上，整个算法的时间复杂度为 O(n)。

2. 空间复杂度

索引映射表 indexMap 需要存储 n 个元素，因此空间复杂度为 O(n)。
递归调用栈的最大深度为树的高度，最坏情况下树完全不平衡，高度为 O(n)，因此递归的最大空间复杂度为 O(n)。
综上，整个算法的空间复杂度为 O(n)。

五、总结知识点

哈希表（HashMap）：用于存储中序遍历中每个值对应的索引，以便快速查找根节点在中序遍历中的位置。
递归：构建二叉树的过程是通过递归函数 buildTree 实现的，每次递归处理一个子树，直到子树为空。
二叉树的构建：理解二叉树的结构和构建过程，以及中序遍历和后序遍历的特点。
数组的索引操作：通过数组的索引来访问和操作数组中的元素，以及计算子数组的长度和位置。
树的节点定义：使用 TreeNode 类来定义树的节点，每个节点包含值 val 和指向左右子节点的引用 left 和 right。
函数的定义和调用：定义了两个函数 buildTree 和 buildTree(int[] postorder, int postStart, int postEnd, int[] inorder, int inStart, int inEnd)，并理解它们之间的调用关系。
边界条件的判断：在递归函数中，首先检查递归的基本情况（即递归的终止条件），如果 postStart > postEnd || inStart > inEnd，则返回 null。
分治思想：将大问题分解为小问题来解决，这里是根据中序遍历和后序遍历的特点，将问题分解为构建左右子树的问题。

以上就是解决这个问题的详细步骤，希望能够为各位提供启发和帮助。