前言：

个人复习整理的笔记，由于是国外教材，故译的数学名词可能与国内教材有些许出入。

目录

​​Ⅰ. 条件概率（condition probability ）​​

​​0x00 定义​​

​​0x01 补充​​

​​Ⅱ.  乘法法则（Multiplication Law）​​

​​0x00 公式​​

​​0x01 证明​​

​​Ⅲ.  事件的独立性（Independence of events）​​

​​0x00 独立（independent）​​

​​0x01 相互独立与相互依赖（independent and dependent）​​

​​0x02 两两独立（pairwisely independent​​

Ⅰ. 条件概率（condition probability ）

0x00 定义

在概率事件（

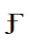
）中，

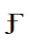  且 

 时，事件 

 已经发生的前提下发生事件 

 的概率： 

  ，我们称之为条件概率。

0x01 补充

集合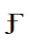上定义的函数：  

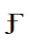
    ，为概率函数。（A1）对于所有 

 ，

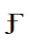 （A2）

（A3）两两互斥事件：

  ， 则（  

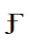
 ）  为概率空间。

Ⅱ.  乘法法则（Multiplication Law）

0x00 公式

（1）对于事件 

 ， 

 时， 

（2）对于事件 

 ，

 时， 

（3）对于事件 

 ，

 时，

0x01 证明

（1） 

（2） 

Ⅲ.  事件的独立性（Independence of events）

0x00 独立（independent）

对于事件 

，

 时，如果 

  ，我们称事件

 与事件 

 独立。

0x01 相互独立与相互依赖（independent and dependent）

对于事件

，如果 

 ，我们称A和B相互独立（independent）。

如果A和B不相互独立，我们称A和B 相互依赖（dependent）。

（1）如果 

 和 

 相互独立，

 和 

 也相互独立。

（2）如果 

 且 

， 

 和 

 相互独立。

（3）如果 

，  

 和 

 互斥，则   

 和 

 相互依赖。

0x02 两两独立（pairwisely independent）

（1）对于所有 

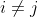
 ，如果 

，         事件 

  称为 两两独立（pairwisely independent）。（2）对于所有  

 ，如果 

，         事件 

 称为 独立（independent）。