DGCN论文阅读

1. 网络架构

本文的主要思想：
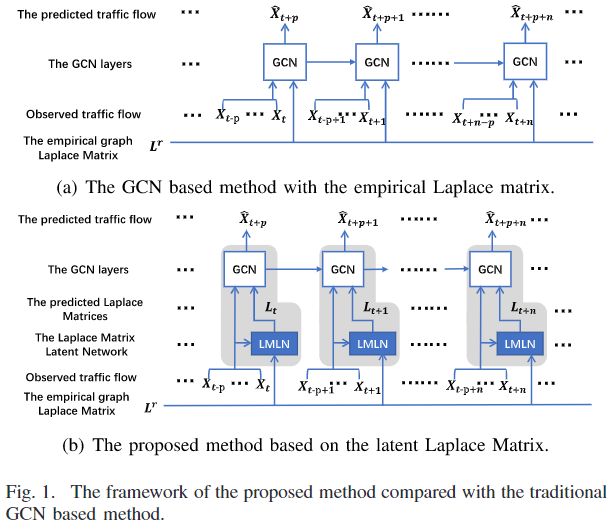
在这里插入图片描述

DGCN的网络框架：
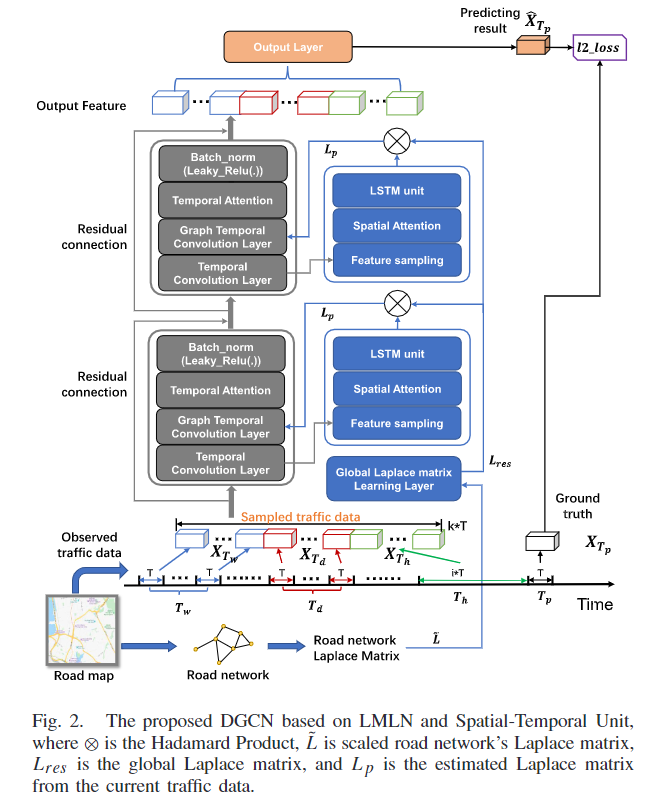
在这里插入图片描述

输入由三部分组成：1. the recent-period data X_Th
2. the daily-period data X_Td；
3. the weekly-period data X_Tw

网络主要由两个部分组成：1. LMLN（蓝色部分）和 2. GCN（灰色部分）

1.1 LMLN，Laplace Matrix Latent Network

看Fig. 2. 蓝色的部分，主要有一个Global Laplace matrix Learning Layer 和两个Laplace matrix prediction unit组成。

Laplace matrix prediction unit的结构如下，主要包括三个部分：1. the feature sampling; 2. the spatial attention; 3. LSTM unit ：
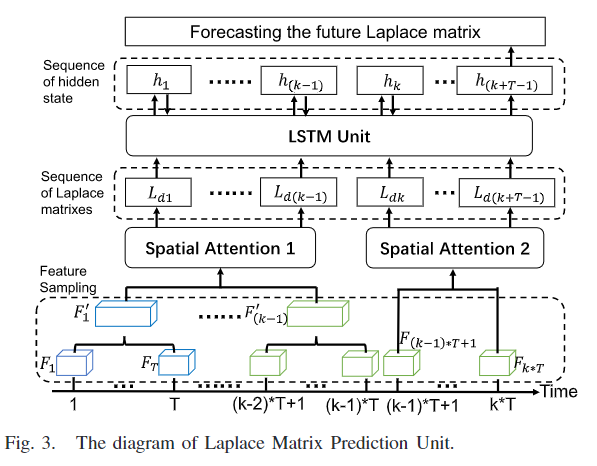
在这里插入图片描述

（1）Global Laplace Matrix Learning Layer*

（提到了参考文献17，maybe思路是从那里来的。）

这里进行了这样的一个数学运算：
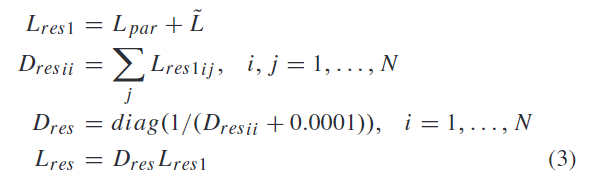
在这里插入图片描述

（2）Feature Sampling

这个模块的目的是：to reduce the data dimension of the traffic feature according to the importance of different time interval

把输入的数据按照时间维度分为k组，每组长度为T。除了最近的T个特征，其余的k-1组都将T步长的特征融合为1个。

前k-1组的操作可以表示为：
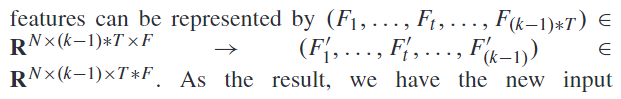
在这里插入图片描述
经过Feature Sampling，数据的维度变成这样：

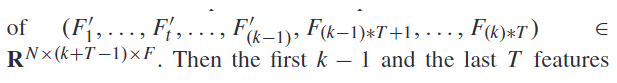
然后融合后的k-1个特征和最后的这个T个特征会通过两个不同的Spatial Attention继续学习。

（3）Spatial Attention

Spatial Attention的计算借鉴了Transformer中self-attention的思想，但是具体的计算不同：
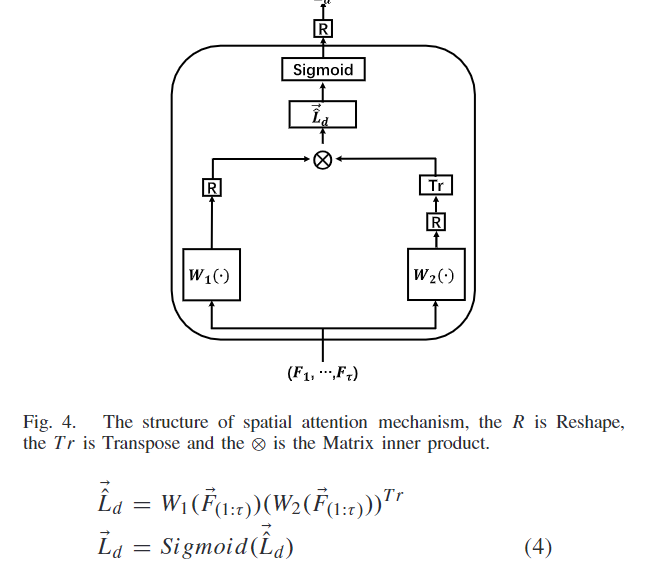
在这里插入图片描述
融合后的k-1个特征经过注意力机制产生k-1个邻接矩阵：

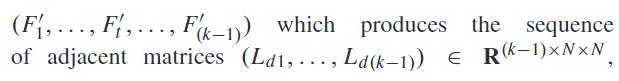
最后的T个特征经过注意力机制产生T个邻接矩阵：

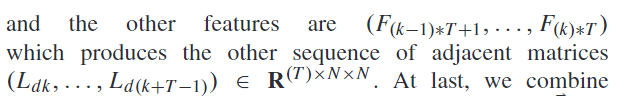
最终该层的输出是k+T-1个邻接矩阵：
$[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-Cxl8Voju-1646383434482)(C:\Users\admin\AppData\Roaming\Typora\typora-user-images\image-20220303161913550.png)]$

（4） LSTM Unit

将k+T-1个N×N的拉普拉斯矩阵沿着时间轴通过LSTM进行融合，LSTM就是一个普通的LSTM：
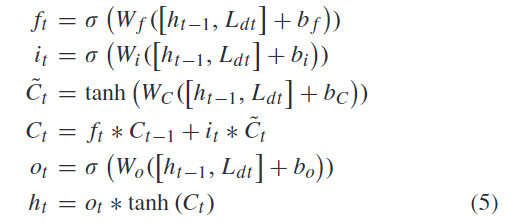
在这里插入图片描述

通过LSTM我们得到了Laplace matrix prediction unit的最终输出h_k+T-1

再与Global Laplace Matrix Learning Layer的输出 global Laplace matrix L_res结合，就得到了 Laplace matrix prediction network 的输出 L_p：
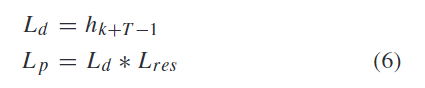
在这里插入图片描述
LMLN的算法可以总结为如下伪代码：

1.2 GCN

GCN是Fig. 2. 中的灰色部分，主要有4个部分。

（1）Temporal Convolution Layer

本模块的目的：to extract the high-dimensional local temporal information from the original traffic data.

对于输入，TCL的运算可以表示为：
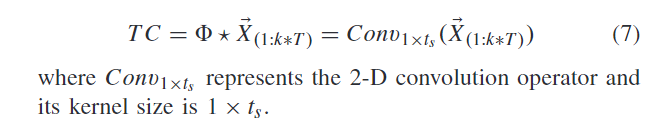
在这里插入图片描述

（2） Graph Temporal Convolution Layer*

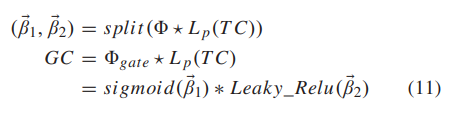
（3） Temporal Attention*

这里是借鉴了参考文献[19]中的Temporal Attention，目的是to explore the long-range time relation。

其运算公式为：
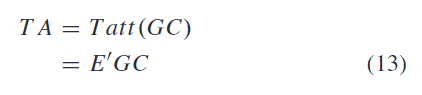
在这里插入图片描述
其中:

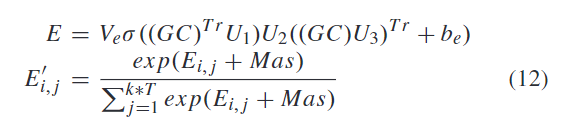
(4)Batch norm

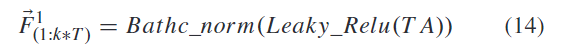
在这里插入图片描述

GCN模块整体的运算过程如下：
在这里插入图片描述

1.3 Loss Function

Output Layer 对 recent data、 daily-period data、 weekly-period data 分开处理。

主要是 recent data是连续的，而 daily-period data和weekly-period data经过了sample处理，被切分成k-i个单元，在时间轴上不连续。

所以使用： Conv_1×i to deal with the recent data, Conv_1×1 to reflect the k − i feature unit dependently in the daily-period and weekly-period.

最后我们将所有convolution output看作我们模型的预测，采用l2_loss计算损失。
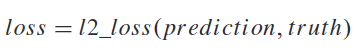
在这里插入图片描述

2. 实验

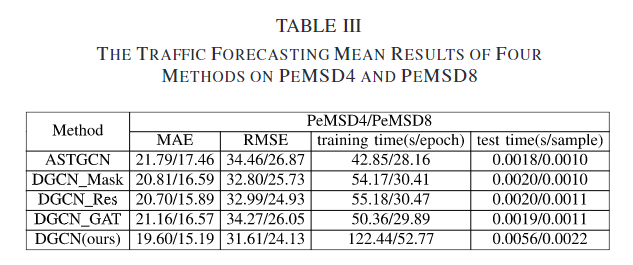
2.1 实验结果

GCRN：Y. Seo, M. Defferrard, P. Vandergheynst, and X. Bresson, “Structured sequence modeling with graph convolutional recurrent networks,” in Proc. Int. Conf. Learn. Represent. (ICLR), 2017, pp. 362–373.

Gated-STGCN：B. Yu, H. Yin, and Z. Zhu, “Spatio-temporal graph convolutional networks: A deep learning framework for traffic forecasting,” in Proc. Int. Joint Conf. Artif. Intell., Jul. 2018, pp. 1–9.

ASTGCN： S. Guo, Y. Lin, N. Feng, C. Song, and H. Wan, “Attention based spatialtemporal graph convolutional networks for traffic flow forecasting,” in Proc. Assoc. Advance Artif. Intell. Conf.(AAAI), 2019, pp. 922–933.

2.2 消融实验

在这里插入图片描述

2.4

在这里插入图片描述

2.5

在这里插入图片描述

3. Introduction

本文的研究动机：Thus, a data-driven method [17] was proposed to optimize a parameterized global-temporal-sharing Laplace matrix in the network training phase, and it obtained richer space connections compared to the empirical one [15], [16]. But, this graph’s Laplace matrix is still fixed in the prediction phase, which cannot capture the dynamic information of the graph to improve the forecasting accuracy.

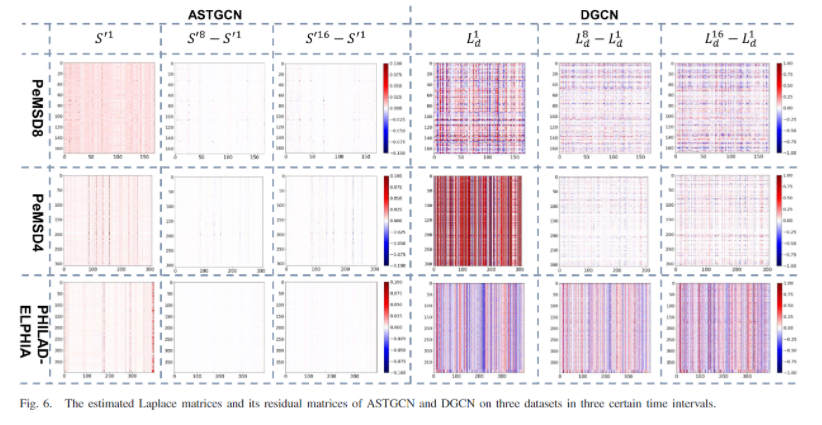
本文的一个比较重要的灵感提供文：AAAI19 ASTGCN：attention mechanism based Spatial-Temporal Graph Convolutional Network (ASTGCN) [18] was presented, in which a dynamic Laplace matrix of the graph was constructed at each input sequence data by the spatial attention mechanism [19].

ASTGCN的两个缺点：①it still utilized the empirical Laplace matrix [15], [16] as a mask；② ASTGCN ignored the inner temporal connection between Laplace matrices of the adjacent periods.