【sklearn练习】KMeans ---- Seeds（小麦种子）数据集聚类评估

文章目录

• ​​一、数据集探索​​
• ​​二、数据预处理​​
• ​​三、构建模型获取结果​​
• ​​四、聚类结果可视化​​
• ​​五、聚类模型评估​​

• ​​① 轮廓系数​​
• ​​② 卡林斯基 - 哈拉巴斯指数​​
• ​​③ FMI评价法​​

一、数据集探索

Seeds 数据集存放了不同品种小麦种子的​​区域​​、​​周长​​、​​压实度​​、​​籽粒长度​​、​​籽粒宽度​​、​​不对称系数​​、​​籽粒腹沟长度​​以及类别数据。该数据集总共210条记录、7个特征、一个标签，标签分为3类。

# 1.读取数据集
data = pd.read_csv("./data/seeds_datas.csv")
x = data.iloc[:,1:8]
target = data.iloc[:,-1]

X:

target:

​​返回顶部​​

二、数据预处理

• 不同特征之间往往具有不同的量纲，由此所造成的数值间的差异可能很大，在涉及空间距离计算或梯度下降法等情况的时候不对其进行处理会影响到数据分析结果的准确性。为了消除特征之间的量纲和取值范围差异可能会造成的影响，需对数据进行标准化处理，也可以称为规范化处理。
• 在这里我们对数据集进行标准差标准化处理。

# 2.对数据集进行离差标准化处理
MMS = MinMaxScaler().fit(x)
x_ = MMS.transform(x)

处理后的数据集：

​​返回顶部​​

三、构建模型获取结果

# 3.构建KMeans聚类模型
cluster = KMeans(n_clusters=3,random_state=123).fit(x_)
# 3.1 获取聚类质心
center = cluster.cluster_centers_
# [[0.75733298 0.79374354 0.69419238 0.73003765 0.76950062 0.36757645,  0.75709318], [0.1233337  0.17513685 0.37817899 0.18671025 0.16252742 0.49856915,  0.27928792], [0.38349003 0.4198407  0.67120387 0.36468534 0.46849918 0.26417688,  0.31838389]]
# 3.2 获取聚类标签
pre_target = cluster.labels_
# 3.3 获取簇内平方和
inertia = cluster.inertia_ # 22.024363075666038

​​返回顶部​​

四、聚类结果可视化

• 这里我们的数据集是多维（包含七个特征），我们需要对其进行降维处理，降到二维平面使用散点图来进行展示。
• 这里的降维采用TSNE。t-SNE(t-distributed stochastic neighbor embedding)是用于降维的一种机器学习算法，是由 Laurens van der Maaten 等在08年提出来。此外，​​t-SNE 是一种非线性降维算法，非常适用于高维数据降维到2维或者3维，进行可视化​​。

# 4.聚类结果可视化
from sklearn.manifold import TSNE
# 4.1 降维处理数据
tsne = TSNE(n_components=2,init='random',random_state=144).fit(x_)
df = pd.DataFrame(tsne.embedding_)
df['labels'] =

• 降维后的数据集

df1 = df[df['labels'] == 0]
df2 = df[df['labels'] == 1]
df3 = df[df['labels'] == 2]
# 绘制画布
fig = plt.figure(figsize=(9,6))
plt.plot(df1[0],df1[1],'bo',df2[0],df2[1],'r*',df3[0],df3[1],'gD')
plt.show()

​​返回顶部​​

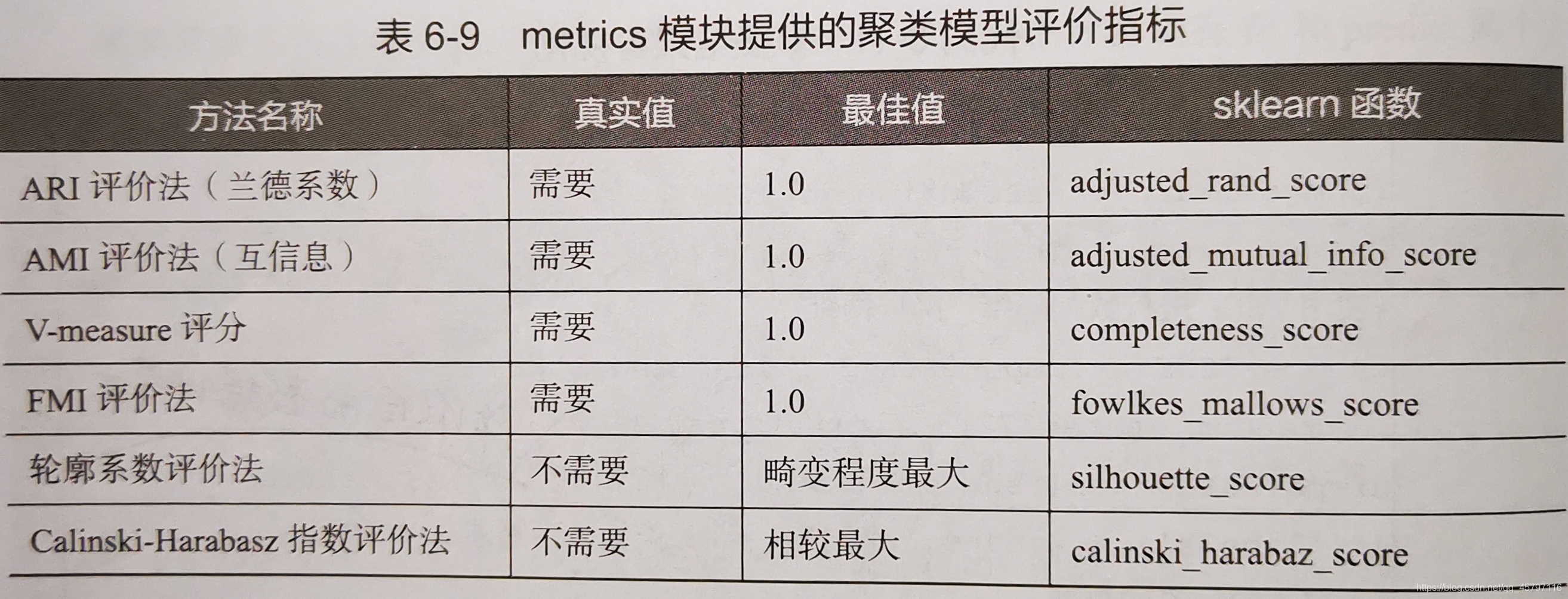
五、聚类模型评估

​​KMeans聚类模型评估指标参见：【skLearn 聚类算法】KMeans​​

① 轮廓系数

# 5.1 轮廓系数法
from sklearn.metrics import silhouette_score
silhouetteScore = []
for i in range(2,15):
    # 构建聚类模型
    kmeans = KMeans(n_clusters=i,random_state=111).fit(x_)
    score = silhouette_score(x_,kmeans.labels_)
    silhouetteScore.append(score)
plt.figure(figsize=(10,8))
plt.plot(range(2,15),silhouetteScore,linewidth=1.5,linestyle='-')
plt.axvline(x=3, color="red", linestyle="--")
plt.axvline(x=4, color="red", linestyle="--")
plt.show()

• 在这里我们获取轮廓系数​​score是所有样本的轮廓系数均值​​，如果要获取每个样本的轮廓系数应当使用​​silhouette_samples​​。这里是​​针对超参数k(n_cluster)​​，所以采用轮廓系数均值进行评估。
• 聚类数目为2、3和3、4的时候，图形的畸变程度最大。本身数据集就是关于3类小麦种子的，侧面说明了聚类为3的时候效果较好。

​​返回顶部​​

② 卡林斯基 - 哈拉巴斯指数

# 5.2 卡林斯基-哈拉巴斯指数
from sklearn.metrics import calinski_harabasz_score
chs = []
for i in range(2,15):
    # 构建聚类模型
    kmeans = KMeans(n_clusters=i,random_state=112).fit(x_)
    chsScore = calinski_harabasz_score(x_,kmeans.labels_)
    chs.append(chsScore)
plt.figure(figsize=(10, 8))
plt.plot(range(2, 15), chs, linewidth=1.5, linestyle='-')
plt.show()

• 由图可以看出，当​​n_cluster=2、3​​的时候，FMI评分都较高，聚类效果也都相对较好。

​​返回顶部​​

③ FMI评价法

# 5.3 FMI评价法 --- 需要有真实标签
from sklearn.metrics import fowlkes_mallows_score
fms = []
for i in range(2,15):
    # 构建聚类模型
    kmeans = KMeans(n_clusters=i,random_state=112).fit(x_)
    fmsScore = fowlkes_mallows_score(target,kmeans.labels_)
    fms.append(fmsScore)
plt.figure(figsize=(10, 8))
plt.plot(range(2, 15), fms, linewidth=1.5, linestyle='-')
plt.show()

• 由图可以看出，当​​n_cluster=3​​的时候，FMI评分最高，聚类效果较好。

​​返回顶部​​