leetcode：106. 从中序与后序遍历序列构造二叉树（JavaScript）-CFANZ编程社区

文章目录

思路：
要点：循环不变量
要点：子树后序遍历序列的起点、终点如何确定
循环不变量是后序序列左闭右开代码
循环不变量是后序序列左闭右闭代码

106. 从中序与后序遍历序列构造二叉树

给定两个整数数组 inorder 和 postorder ，其中 inorder 是二叉树的中序遍历， postorder 是同一棵树的后序遍历，请你构造并返回这颗 二叉树 。

示例 1:

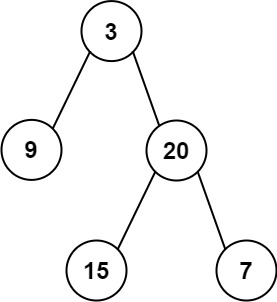
输入：inorder = [9,3,15,20,7], postorder = [9,15,7,20,3]
输出：[3,9,20,null,null,15,7]

示例 2:

输入：inorder = [-1], postorder = [-1]
输出：[-1]

提示:

1 <= inorder.length <= 3000
postorder.length == inorder.length
-3000 <= inorder[i], postorder[i] <= 3000
inorder 和 postorder 都由不同的值组成
postorder 中每一个值都在 inorder 中
inorder 保证是树的中序遍历
postorder 保证是树的后序遍历

思路：

首先要明白后序遍历的序列最后一个元素一定是当前序列二叉树的根元素，如[9,15,7,20,3]3就是根节点，所以第一步我们需要在中序遍历序列中找到3的位置，然后将中序遍历序列分割成左右两部分[9], [3,15,20,7]，即左子树、右子树，再找到左右子树后序遍历序列的最后一个元素在中序遍历序列中的位置，继续分割，直到找到叶子节点，返回该节点，层层返回给上一级（回溯）就构建好了目标二叉树。可以看出分割数组的过程是高度重复的工作，以及它需要回溯的特点，所以很适合用递归来写。

要点：循环不变量

什么是循环不变量，简单来说就是在整个循环过程中不变的东西，在使用递归方法时一定明确什么是不变的，否则递归过程很容易变得混乱不堪，下面的代码循环不变量就是取序列时左闭右开，例如在第一次处理左子树时后序序列为[9, 3),但是3并不是左子树的结点，它是根节点。确定循环不变量并没有什么统一的规则，自己决定就好，但是一旦决定了，整个代码就要遵循这一规则。

要点：子树后序遍历序列的起点、终点如何确定

首先要明白分割后的左子树中序序列，后序序列长度一定相同，如果明白这点那就好办了，当处理左子树时，后序遍历序列起点就是原来的起点，终点就是原来的起点加上左子树的长度，如：第一次处理左子树时中序序列为[9]，postorderstart = 0; index = 1; postorderend = 0 + 1 - 0 = 1，后序序列为[9,3)，处理右子树时，后序遍历序列起点就是原来的起点加上左子树的长度，终点就是原来的终点减一，因为最后一个元素是当前序列的根节点，在处理子树时肯定要舍弃。

注意：我给出的代码实际上并没有真正的分割数组，使用一个头指针一个尾指针模拟的数组分割，如果想要真正分割数组的代码可以去代码随想录看看。

循环不变量是后序序列左闭右开代码

var buildTree = function(inorder, postorder) {
    return dfs(inorder, postorder, 0, inorder.length, 0, postorder.length)
};
var dfs = function(inorder, postorder, inorderstart, inorderend, postorderstart, postorderend) {
    // 子树为空，返回bull
    if (postorderstart >= postorderend) return null;
    // 条件符合，是叶子节点
    if (postorderend - postorderstart === 1) {
        return new TreeNode(postorder[postorderend - 1]);
    }
    // 取后序序列最后一个元素即根节点
    // 因为循环不变量是左闭右开，所以下标要减一才是当前序列根节点
    const value = postorder[postorderend - 1];
    // 在中序序列中查找根元素
    const index = inorder.indexOf(value);
    // 构造当前节点
    const root = new TreeNode(value);
    // 处理左子树
    root.left = dfs(inorder, postorder, inorderstart, index, postorderstart, postorderstart + index - inorderstart);
    // 处理右子树
    root.right = dfs(inorder, postorder, index + 1, inorderend, postorderstart + index - inorderstart, postorderend - 1)
    return root;
}

循环不变量是后序序列左闭右闭代码

var buildTree = function(inorder, postorder) {
    return dfs(inorder, postorder, 0, inorder.length - 1, 0, postorder.length - 1)
};
var dfs = function(inorder, postorder, inorderstart, inorderend, postorderstart, postorderend) {
    if (postorderstart > postorderend) return null;
    if (postorderend === postorderstart) {
        return new TreeNode(postorder[postorderend]);
    }
    // 取后序序列最后一个元素即根节点
    // 因为循环不变量是左闭右开，所以下标要减一才是当前序列根节点
    const value = postorder[postorderend];
    const index = inorder.indexOf(value);
    const root = new TreeNode(value);
    
    root.left = dfs(inorder, postorder, inorderstart, index - 1, postorderstart, postorderstart + index - inorderstart - 1);
    root.right = dfs(inorder, postorder, index + 1, inorderend, postorderstart + index - inorderstart, postorderend - 1)
    return root;
}