文章目录
一、跳跃表的概念
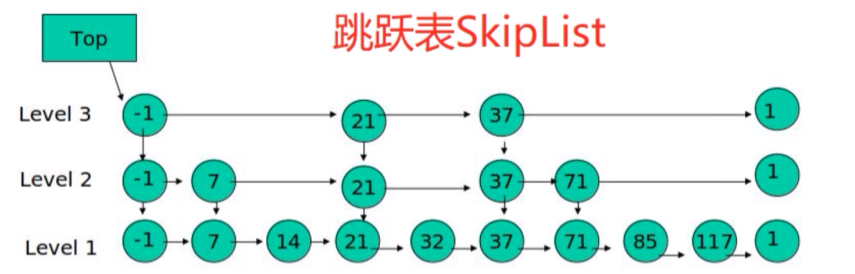
跳跃表具有如下性质:
- 由很多层链表组成,每一层都是一个有序链表
- 最底层(level 1)的链表包含所有元素
- 如果一个元素出现在level i层的链表中,则它在level i之下的链表也都会出现
- 每个节点都包含两个指针,一个指向同一链表中的下一个元素,一个指向下面一层的元素跳跃表的增加、删除、查询操作时间复杂度和红黑树一样,也是 O ( l o g 2 N ) O(log_2N) O(log2N)
相比于红黑树,它的优势是:
- 实现起来更加简单
- 跳跃表的增加、删除操作只会改动局部,不像红黑树的增加、删除操作,因为需要节点重新着色和旋转,可能整棵树都要进行调整,这就导致了并发环境下红黑树锁的粒度大。并发环境下,跳跃表只需要对插入元素影响的区间加锁即可,跳跃表加锁的粒度会更小一些,并发能力更强
- 因为跳跃表的每一层都是一个有序的链表,因此范围查找非常方便,优于红黑树的范围搜索的跳跃表相比于红黑树,是用空间换时间(level 2层开始每一层都有会存储重复的数据),因此占用的内存空间比红黑树大
跳跃表相对于红黑树而言,是在空间换时间,占用内存比较大。红黑树中,所有元素值只是存储一个节点的,但是在跳跃表中,所有的元素不仅仅在最下面那层出现,而且根据抛硬币选出来的元素在上面层进行存储,以此类推上去,模拟了一个二分查找搜索树的过程,简化了红黑树,达到O(logn)的搜索和删除的时间复杂度,而且实现起来比较简单
在实际应用场景中,跳跃表和红黑树在很多情况下是可以互换的
redis的有序集合也是用SkipList实现的,增、删、查都是
O
(
l
o
g
2
N
)
O(log_2N)
O(log2N),只要能定义比较方式,就可以用SkipList存储
关于SkipList的层数,我们采用符合二项分布的函数确定是否将某个节点存储至上一层。既然是符合二项分布,当数据量较大时,一般来说对于相邻两层,上层节点数量会是下层节点数量的 1 / 2 1/2 1/2,这就很类似于二叉树了

二、跳跃表的find
我们查找117的过程如下:
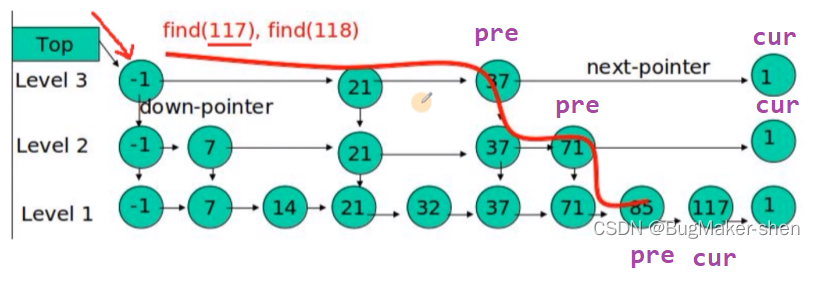
- 先在最上层的链表找第一个大于117的数,从这个大于117节点的前一个节点往下寻找,于是从37往下查找
- 同理,从71往下找
- 在最下层节点找到117
bool find(int data) const{
Node* pre = head_;
Node* cur = pre->next_;
while (true) {
if (cur != nullptr) {
if (cur->data_ < data) {
pre = cur;
cur = cur->next_;
}
else if (cur->data_ > data) {
if (pre->down_ == nullptr) {
// 已经到了level 1
return false;
}
pre = pre->down_;
cur = pre->next_;
}
else {
return true;
}
}
else {
// cur == nullptr
if (pre->down_ == nullptr) {
// 已经到了level 1
return false;
}
else {
pre = pre->down_;
cur = pre->next_;
}
}
}
}
三、跳跃表的insert
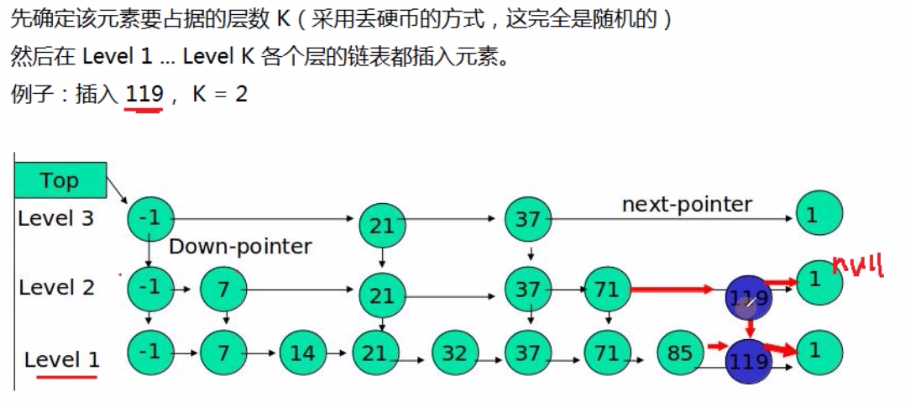
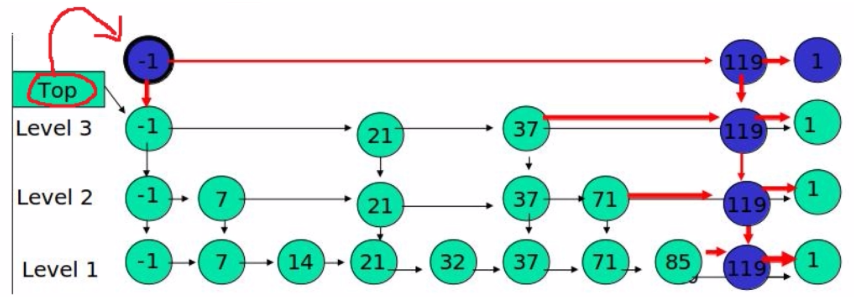
如果我们要插入119这个数字,通过抛硬币,决定119要插几行
- K=2:跳表本身是3行,插2行是没有问题的,在最后一行按序插入,因为要插2行,所以在第二行也插了一个119
- K=4:跳表只有3层,但是最终我们也是要插4层的,也就是说,在最上层(第4层)就只有一个数字119
- K=5:119这个数字要添加到5层,但是跳表只有3层,所以我们最终也是只插4层就可以了

编写代码顺序:
- 查找data,重复则不插入
- 获取level,若level过大,调整level使得skiplist只增长一层
- 用数组存储要插入的level个节点,并纵向连接
- 找到最先插入节点的第level层链表的头节点,往后遍历找到合适的位置插入数组中的节点,然后再到下层链表找到合适的位置插入,直到在底层链表插入
void insert(int data) {
if (find(data)) {
// 不插入重复数据
return;
}
int level = get_level();
if (level > head_->level_) {
// level过大,只增长一层
level = head_->level_ + 1;
// 需要增长,则构造新的头节点
HeadNode* new_head = new HeadNode(level);
new_head->down_ = head_;
head_ = new_head;
}
// 先创建一个指针数组,用于存放data节点的地址
Node** new_nodes = new Node * [level];
for (int i = level - 1; i >= 0; i--) {
new_nodes[i] = new Node(data);
if (i != level - 1) {
new_nodes[i]->down_ = new_nodes[i + 1];
}
}
// 若获取的level本身很小,需要将insert_head指向首次插入的层
Node* insert_head = head_;
for (int i = head_->level_; i > level; i--) {
insert_head = insert_head->down_;
}
Node* pre = insert_head;
Node* cur = pre->next_;
for (int i = 0; i < level; i++) {
while (cur != nullptr && cur->data_ < data) {
// 找第一个大于data的节点
pre = cur;
cur = cur->next_;
}
// 找到第一个大于data的节点后,将数组内存放的data节点插入pre和cur之间
new_nodes[i]->next_ = cur;
pre->next_ = new_nodes[i];
pre = pre->down_;
if (pre != nullptr) {
cur = pre->next_;
}
}
delete[] new_nodes;
new_nodes = nullptr;
}
四、跳跃表的remove
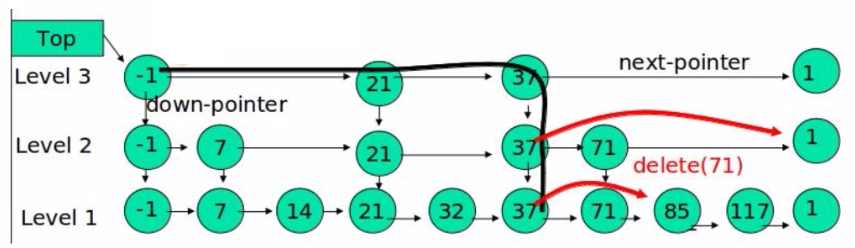
- 删除71:先查找到level 2的71,修改37节点的指针域,然后把71这一整列的节点全部delete
- 删除37:在level 3中找到37,修改37前面节点的指针域,并把37这一整列的节点全部delete
需要注意:如果此时链表的最高层只有一个数据节点119,我们在删除操作中把最高层的数据节点119删除了,那么此时最高层链表就只剩一个头节点了,而这个头节点也是要删除的
编写代码顺序:
- 查找第一个data的数据,现在上层链表找第一个大于data的节点,找到则删除,并且pre向下走;找不到则pre直接向下走
- 在同一层链表查找data时,一直向后遍历,直到找到data或cur为空
void remove(int data) {
// 头节点不可能为空
Node* pre = head_;
Node* cur = pre->next_;
while (true) {
if (cur != nullptr) {
if (cur->data_ < data) {
pre = cur;
cur = cur->next_;
continue;
}
else if (cur->data_ == data) {
pre->next_ = cur->next_;
delete cur;
if (head_->next_ == nullptr) {
// 如果只剩头节点了,说明pre肯定也指向头节点
delete head_;
head_ = static_cast<HeadNode*>(pre);
}
}
}
// 这里 (cur==nullptr) || (删除节点了pre准备向下走) || (找到了第一个大于data的节点,pre准备向下走)
if (pre->down_ == nullptr) {
// 已经到了level 1,且cur==nullptr,说明已经遍历到最右下角的节点了
return;
}
pre = pre->down_;
cur = pre->next_;
}
}
五、完整代码
class SkipList {
public:
SkipList() {
head_ = new HeadNode(1); // 跳跃表初始化为第一层
}
~SkipList() {
Node* next_head = head_;
int level = head_->level_;
for (int i = level; i > 0; i--) {
Node* pre = next_head;
Node* cur = pre->next_;
next_head = next_head->down_;
while (cur != nullptr) {
delete pre;
pre = cur;
cur = cur->next_;
}
}
}
bool find(int data) const{
Node* pre = head_;
Node* cur = pre->next_;
while (true) {
if (cur != nullptr) {
if (cur->data_ < data) {
pre = cur;
cur = cur->next_;
}
else if (cur->data_ > data) {
if (pre->down_ == nullptr) {
// 已经到了level 1
return false;
}
pre = pre->down_;
cur = pre->next_;
}
else {
return true;
}
}
else {
// cur == nullptr
if (pre->down_ == nullptr) {
// 已经到了level 1
return false;
}
else {
pre = pre->down_;
cur = pre->next_;
}
}
}
}
void insert(int data) {
if (find(data)) {
// 不插入重复数据
return;
}
int level = get_level();
if (level > head_->level_) {
// level过大,只增长一层
level = head_->level_ + 1;
// 需要增长,则构造新的头节点
HeadNode* new_head = new HeadNode(level);
new_head->down_ = head_;
head_ = new_head;
}
// 先创建一个指针数组,用于存放data节点的地址
Node** new_nodes = new Node * [level];
for (int i = level - 1; i >= 0; i--) {
new_nodes[i] = new Node(data);
if (i != level - 1) {
new_nodes[i]->down_ = new_nodes[i + 1];
}
}
// 若获取的level本身很小,需要将insert_head指向首次插入的层
Node* insert_head = head_;
for (int i = head_->level_; i > level; i--) {
insert_head = insert_head->down_;
}
Node* pre = insert_head;
Node* cur = pre->next_;
for (int i = 0; i < level; i++) {
while (cur != nullptr && cur->data_ < data) {
// 找第一个大于data的节点
pre = cur;
cur = cur->next_;
}
// 找到第一个大于data的节点后,将数组内存放的data节点插入pre和cur之间
new_nodes[i]->next_ = cur;
pre->next_ = new_nodes[i];
pre = pre->down_;
if (pre != nullptr) {
cur = pre->next_;
}
}
delete[] new_nodes;
new_nodes = nullptr;
}
void remove(int data) {
// 头节点不可能为空
Node* pre = head_;
Node* cur = pre->next_;
while (true) {
if (cur != nullptr) {
if (cur->data_ < data) {
pre = cur;
cur = cur->next_;
continue;
}
else if (cur->data_ == data) {
pre->next_ = cur->next_;
delete cur;
if (head_->next_ == nullptr) {
// 如果只剩头节点了,说明pre肯定也指向头节点
delete head_;
head_ = static_cast<HeadNode*>(pre);
}
}
}
if (pre->down_ == nullptr) {
// 已经到了level 1,且cur==nulptr,说明已经遍历到最右下角的节点了
return;
}
pre = pre->down_;
cur = pre->next_;
}
}
void show() const {
Node* head = head_;
while (head != nullptr) {
Node* cur = head->next_;
while (cur != nullptr) {
cout << cur->data_ << " ";
cur = cur->next_;
}
cout << endl;
head = head->down_;
}
cout << endl;
}
private:
int get_level() {
int n = 1;
while (rand() % 2 == 1) {
n++;
}
return n;
}
private:
// 普通节点类型
struct Node {
Node(int data = 0)
: data_(data)
, next_(nullptr)
,down_(nullptr)
{}
int data_;
Node* next_;
Node* down_;
};
// 头节点类型
struct HeadNode : public Node {
HeadNode(int level)
: level_(level)
{}
int level_; // 记录跳跃表的层数
};
private:
HeadNode* head_;
};
