Abstract

本文将讨论分布空间的Natrual Gradient, 然后将Natural Gradient 用于Actor Critic。另外说明Trust Region Policy Optimization(TRPO) 和 Proximal Policy Optimization(PPO)算法。

Part One: Basic Knowledge in Natural Gradient

参数空间更新的缺点：

当我们用有限的参数去模拟一个函数时，即使我们对一个参数进行很小的更改，我们每次的改变有时候也是巨大的。

例如下图，图中均为正态分布，左图分别是 N(0,0.2),N(1,0.2) ，而右图中分别是 N(0,10),N(1,10) 。在参数空间中左右两图的两条曲线的欧拉距离都是1( $d=\sqrt{(\mu_0-\mu_1)^2+(\sigma_0-\sigma_1)^2}$ ). 但是我们可以明显看出左图的两条曲线相似度较差，而右图中的相似度较高。因此，在参数空间中对参数进行直接改变，即使是参数更改很小，有时也会引起策略的很大变化。而策略的巨大变化会引起学习的不稳定。另外我们在Actor-critic methods中策略每次变化的较小，value function每次能够及时更新，和当前策略进行匹配。当策略变化较大时，value function将难以对应当前政策，使得更新方向出现巨大偏差，不会得到最优解。

为了解决上述参数空间中的问题，我们需要引入分布空间，也就是实际分布所在的空间。实际分布所在的空间就是关注的物理量在数值上的分布。同时需要引入测量两个分布相似程度的物理量。

KL(Kullback-Leiber) divergence

为了对两个分布p和q的相似程度进行描述，我们引入了KL Divergence的测量。

我们将在分布空间中进行积分（实际过程中将进行sampling，然后求和），然后将每个点的结果叠加。我们可以看到如果p和q完全相同，KL Divergence将是0。另外我们可以看到KL Divergence是不对称的， $D_{KL}(p||q) \neq D_{KL}(q||p)$ ，但是当p和q很接近时，两者是近似相等的。

当然，我们也可以引入Jensen-Shannon(JS) Divergence，消除这种不对称性：

当然，当p和q很接近时， $D_{KL}(p||q)\approx D_{JS}(p||q)$

参数空间和分布空间之间的联系： Fisher Matrix

我们实际通过操控 $\Delta \theta$ 在参数空间改变策略，但是我们需要保证相邻步的策略在分布空间中相似度较高，一直小于我们的设定值 $\delta$ 。因此我们需要建立 $\Delta \theta$ 和 KL Divergence之间的关系。

对于第一项 $\bigtriangledown_{\theta'} D_{KL}[p(x;\theta)||p(x;\theta +\Delta \theta)] =\bigtriangledown_{\theta'} E_{p(x;\theta)}[log \ p(x;\theta)]- \bigtriangledown_{\theta'}E_{p(x;\theta)}[log \ p(x;\theta+\Delta \theta)]$

而其中

因此，

因此分布空间中相邻两个策略的相似度和 $\Delta \theta$ 之间的关系就建立起来了。但是我们仍然需要知道KL divergence的二阶导数是什么含义。

我们可以得到 $D_{KL}$ 的二阶梯度是 $log \ p(x;\theta)$ 的黑森矩阵的负期望。

而黑森矩阵的负期望则是 Fisher Matrix。

Fisher Information Matrix - Agustinus Kristiadi's Blog

Natural Gradient Descent - Agustinus Kristiadi's Blog

Natural Gradient

Aim

Constraint:

根据凸优化可以得到结果：

而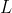具体的函数内容则与natural gradient 无关，因为natrual gradient只是解决了让相邻策略有较强的相似性（改变了参数向量的更新方向），保证学习过程的稳定性。同时natural gradient依赖于曲率的逆，当损失方程处于平坦位置，步长较大；当损失方程处于较陡的区域，步长较小。只不过Fisher Matrix的尺寸随着参数向量的尺寸增大而增大，尺寸是 $N \times N$ ，因此求逆会比较麻烦。因此有时我们使用conjugate gradient,K-FAC等方法计算。

Part Two: Natural Actor Critic

Part Three: Trust Region Policy Optimization TRPO

Objective Function

TRPO中采用的目标函数是 $\eta(\pi_\theta)=E_{\tau \sim \pi_\theta}[\sum_{t=0}^{\infty}\gamma^t r_t]$

$\eta(\pi_{i+1})\\= \eta(\pi_i) + \sum_s \rho_{\pi_{i+1}}(s)\sum_a \pi_{i+1}(a|s)A_{\pi}(s,a)$

证明：

Surrogate Function

TRPO采用Minorize-Maximization Algorithom，在每时刻的参数向量下找一个下边界函数surrogate function，也采用参数向量为参数，在此参数向量下与 $\eta(\pi_\theta)$ 相等，在参数空间的其他参数下小于 $\eta(\pi_\theta)$ 。另外下边界函数需要比原函数便于优化。

因为我们知道下边界函数在当前参数向量下和目标函数相近，因此我们可以知道下边界函数在当前参数向量的附近方向优化方向与目标函数近似，因此我们可以在每时刻都选用一个下边界函数，然后每次对下边界函数进行优化，从而得到目标函数的优化。因此关键就是如何选取下边界函数。

$\eta(\pi_{i+1}) = \eta(\pi_i) + \sum_s \rho_{\pi_{i+1}}(s)\sum_a \pi_{i+1}(a|s)A_\pi(s,a) \approx \eta(\pi_i) + \sum_s \rho_{\pi_i}(s) \sum_a \pi_{i+1}(a|s)A_\pi(s,a) \approx \eta(\pi_i) + \sum_s \rho_{\pi_i}(s) \sum_a \pi_i(a|s) \frac{\pi_{i+1}(a|s)}{\pi_i(a|s)}A_\pi(s,a)$

我们定义函数

$J_{\pi_{i}}(\pi_{i+1}) = \eta(\pi_i) + \sum_s \rho_{\pi_i}(s) \sum_a \pi_i(a|s) \frac{\pi_{i+1}(a|s)}{\pi_i(a|s)}A_\pi(s,a)$

$\bigtriangledown_{\theta} J_{\pi_i}(\theta)|_{\theta=\theta_{old}} =\bigtriangledown_\theta \eta(\theta)|_{\theta = \theta_{old}}$

然后我们再定义surrogate function：

$L(\theta)=J_{\theta_{old}}(\pi_\theta)-C D_{KL}(\pi_{\theta_{old}}||\pi_\theta)$

其中 $C=\frac{4\epsilon \gamma}{(1-\gamma)^2}$

如何看懂TRPO里所有的数学推导细节? - 知乎 (zhihu.com)

此时 $L(\theta)$ 满足以下三个条件：

$L(\theta_{old})=\eta(\theta_{old})$
$\bigtriangledown_\theta L_{\theta_{old}}(\theta)|_{\theta=\theta_{old}}=\bigtriangledown_\theta \eta(\theta)|_{\theta=\theta_{old}}$
$\eta(\theta) \geq J_{\theta_{old}}(\theta)-C D_{KL}(\pi_{\theta_{old}}||\pi_\theta)$

因此 $L(\theta)$ 就是目标函数的一个下边界函数，可以在该参数向量点通过该下边界函数对目标函数进行优化。

直接使用natural gradient 进行优化

aim: $J_{\pi_{i}}(\pi_{i+1}) = \sum_s \rho_{\pi_i}(s) \sum_a \pi_i(a|s) \frac{\pi_{i+1}(a|s)}{\pi_i(a|s)}A_\pi(s,a)$

constraint: $D_{KL}(\pi_{\theta_{old}}||\pi_\theta) < \delta$

但是，为了防止我们得到的新参数向量和原参数向量的 $D_{KL}$ 超过 $\delta$ ，我们采用下式对参数向量进行更新：

j取可以使得相邻策略相似度满足要求的最小非负整数。

TRPO 在全连接层中工作较好，但是在CNN或者RNN中表现较差。

Part Four: Proximal Policy Optimization PPO

针对上述TRPO算法的较差算法复杂度，较高的计算量，PPO通过更改surrogate function来得以优化。

当 $A_{\pi_{\theta_{old}}}(s_t,a_t)$ 为正的时候，说明这是一个更好的动作，我们应该增加其概率，但是为了防止增加的概率太大，我们要进行限制，使得参数向量朝着正确的方向，移动较小的步长，使得相邻的策略都是近似的。当 $A_{\pi_{\theta_{old}}}(s_t,a_t)$ 为负的时候，这是一个应该减少概率的动作，为了防止减少的过多，我们限制其步长。

另外，我们通过clip已经实现了对相邻策略的相似度限制，因此可以避免对KL Divergence的计算，可以减少很多计算量，而是使用SGD(stochastic gradient descent)实现一阶的梯度。同时，因为相邻的策略之间相似度较高，可以不完全满足on-policy的更新方式，可以在多个episodes中更新多次，算法的复杂度大大降低。