1.3
Codeforces Round #763 (Div. 2)
E - Middle Duplication
对于一个字符串,如果这个字符的下一个和它不一样的字符比它大,那么将这个字符分裂成两个,才会使这个字符串的字典序变小。这道题目中,我们称这样的字符是好字符。
对于分裂这个操作,我们想要让结果是字典序最小,那么我们对于分裂好字符是有优先级的——离字符串的起始端越近,好字符的分裂优先级越高,因为字典序的排序方式是从左到右查看字符的ASCII顺序,如果前面某一位字符小了(大了),那么这个字符串的字典序就小了(大了)。所以,离起始端最近的好字符,如果要分裂的话,是一定要最先分裂的。
题目中对于分裂还有一条限制,如果想要分裂这个字符,那么这个字符在一棵树上的父节点的字符需要先被分裂。不过,我们要通过这棵树的中序遍历获取真正的序列。想要找到最先分裂的好字符,我们要尽量在树上向左遍历结点。
需要注意的是,根据分裂在树上的限制,我们可以发现一个性质:如果这个点u没有被确认分裂,那么u的右子树可以不用遍历,因为如果要在右子树找可以分裂的点的话,那么势必u也要被分裂。而u没有被分裂是因为其本身不是好字符,由于这个点的字符在字符串上比下一个与其不同的字符的ASCII码大,所以分裂后只会让整个字符串的字典序变大。
所以,如果最先分裂的好字符处于1号结点的右子树里,那么这个字符串不进行任何分裂。
反之,我们通过dfs中序遍历寻找,那么访问好字符的顺序一定是字符串的顺序。
考虑第二条限制:我们要分裂的字符数量不超过 。我们可以发现,找到一个结点并把它分裂,根据树上限制,我们至少要分裂这个结点所在层数数量的结点。我们可以把分裂这个结点时一共分裂的结点数量当作一个对
。我们可以发现,找到一个结点并把它分裂,根据树上限制,我们至少要分裂这个结点所在层数数量的结点。我们可以把分裂这个结点时一共分裂的结点数量当作一个对 的消耗。我们设
的消耗。我们设![cost[i]](https://file.cfanz.cn/uploads/gif/2022/01/09/16/4LWAA465U8.gif) 是第i个结点如果被分裂,会带来的消耗的数量,即算上自己,这波一共要分裂多少个字符。
是第i个结点如果被分裂,会带来的消耗的数量,即算上自己,这波一共要分裂多少个字符。
那么对于一个访问到的结点:
- 如果这个点的结点编号是0,说明是空的,直接返回。
- 如果这个点的
![cost[i]>k](https://file.cfanz.cn/uploads/gif/2022/01/09/16/G69PHP9W98.gif) ,说明当前的剩余点数已经不足以让这个点被分裂。所以直接返回。
,说明当前的剩余点数已经不足以让这个点被分裂。所以直接返回。 - 根据中序遍历,我们要先访问左子树。访问之前,先令
![cost[l[i]]=cost[i] + 1](https://file.cfanz.cn/uploads/gif/2022/01/09/16/f84WaE7D38.gif) 。如果左孩子要被分裂,那么当前这个结点也要被分裂。
。如果左孩子要被分裂,那么当前这个结点也要被分裂。 - 如果左孩子没有被分裂,但当前这个结点所表示的字符是一个好字符,那么这个字符要被分裂。同时,令
![k=k-cost[i]](https://file.cfanz.cn/uploads/gif/2022/01/09/16/d01I88457S.gif) ,即分裂了这个点,将消耗从
,即分裂了这个点,将消耗从 种减掉。
种减掉。 - 如果这个点被分裂了,令
![cost[r[i]]=1](https://file.cfanz.cn/uploads/gif/2022/01/09/16/3Le5c7W46P.gif) ,因为既然已经往右子树走了,那么前面的左子树的消耗已经清算了,接下来重新开始更新消耗值。然后接着访问右子树。
,因为既然已经往右子树走了,那么前面的左子树的消耗已经清算了,接下来重新开始更新消耗值。然后接着访问右子树。
这样的话, 只需要用一个数组记录这个结点是否被分裂,然后在字符串上遍历。如果这个字符在树上被分裂,那么这个字符就输出两次,否则输出一次。
AC代码:
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
inline LL read() {
LL x = 0, y = 1; char c = getchar();
while (c > '9' || c < '0') { if (c == '-') y = -1; c = getchar(); }
while (c>='0'&&c<='9') { x=x*10+c-'0';c=getchar(); } return x*y;
}
LL n, k, id;
char s[200050], str[200050];
LL l[200050], r[200050];
LL gn[200050], dou[200050];
LL gid[200050], rid[200050];
LL cost[200050];
void dfs(LL x)
{
if (!x) return;
if (cost[x] > k) return;
cost[l[x]] = cost[x] + 1;
dfs(l[x]);
if (dou[l[x]]) dou[x] = 1;
else if (gn[rid[x]])
{
dou[x] = 1;
k -= cost[x];
}
if (dou[x])
{
cost[r[x]] = 1;
dfs(r[x]);
}
}
void tos(LL x)
{
if (x == 0) return;
tos(l[x]);
s[++id] = str[x];
rid[x] = id; gid[id] = x;
tos(r[x]);
}
void main2()
{
n = read(); k = read();
scanf("%s", str + 1);
for (LL i = 1; i <= n; ++i)
{
l[i] = read(); r[i] = read();
gn[i] = cost[i] = dou[i] = 0;
}
id = 0; tos(1);
LL L = 1, R = 1;
for (LL i = 2; i <= n; ++i)
{
if (s[i] > s[i - 1])
{
for (LL j = L; j < i; ++j)
{
gn[j] = 1;
}
L = i;
}
if (s[i] < s[i - 1]) L = i;
}
cost[1] = 1;
dfs(1);
for (LL i = 1; i <= n; ++i)
{
printf("%c", s[i]);
if (dou[gid[i]]) printf("%c", s[i]);
}
}
LL T = 1;
int main()
{
for (LL t = 1; t <= T; ++t)
{
main2();
}
return 0;
}1.4
POJ
2752 - Seek the Name, Seek the Fame
考察对KMP中next函数的理解。
题目中所求的是对于一个字符串,前缀-后缀字符串的所有可能长度。我们在KMP中的next[i]代表P数组从1到i中前缀后缀相同的最大长度。运用到这道题目里面来,题目中虽然要求从小到大输出,但我们可以从大到小求(一句废话)。
首先,最长的答案一定是S字符串本身。因为,对于自己本身,前缀一定等于后缀。
假设S字符串的长度为len,那么next[len]表示这个字符串中完全相同的前缀和后缀的最长的长度。我们设这个前缀是A,后缀是B,有A=B。我们现在要找到S串两端完全相同的长度稍微小一点的前后缀,由于A=B,我们可以把S串后缀端等效成A串的后缀端,那么这样的话我们就只需要看S字符串从1到next[len]这一段的完全相同的前后缀是什么(当然也可以把S的前端等效成B的前端,看S字符串从next[len]+1到len。
(POJ暂时不能评测,所以不知道是不是AC代码,暂时存到这里)
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
char P[400050];
LL nxt[400050];
LL lp, li;
LL len[400050];
void getFail()
{
nxt[1] = 0;
for (LL i = 2; i <= lp; ++i)
{
LL j = nxt[i - 1] + 1;
while (j > 1 && P[i] != P[j]) j = nxt[j - 1] + 1;
nxt[i] = (P[i] == P[j]) ? j : 0;
}
}
void getans(LL x)
{
if (!x) return;
len[++li] = x;
getans(nxt[x]);
}
int main()
{
while (~scanf("%s", P + 1))
{
lp = strlen(P + 1);
getFail();
li = 0;
getans(lp);
sort(len + 1, len + li + 1);
LL l2 = unique(len + 1, len + li + 1) - len - 1;
for (LL i = 1; i <= l2; ++i)
{
printf("%lld ", len[i]);
}
printf("\n");
}
return 0;
}Luogu
P1470 - [USACO2.3]最长前缀 Longest Prefix
题解都是枚举子串,不过感觉KMP+DP既好想又好写。简单来说,就是用KMP将每一个小段与目标的大字符串进行匹配,然后dp求最长的长度。
但因为没仔细读题,被这题的诡异输入方式卡了好久(为什么要一个大长字符串切成几段换行读入……)
AC代码
P3435 - [POI2006]OKR-Periods of Words
我们用+表示字符串的连接。假设 是
是 的周期,那么可以写成
的周期,那么可以写成 ,
, ,将两个等式联立,可得
,将两个等式联立,可得 。其中
。其中 均为字符串。所以我们可得:
均为字符串。所以我们可得: 。
。
我们想要求每一个 的前缀的最长周期
的前缀的最长周期 ,也就是说我们只需要找到最短的
,也就是说我们只需要找到最短的 即可。显然,
即可。显然, 在
在 中是左右对称的。我们很容易想到,这种形式类似于
中是左右对称的。我们很容易想到,这种形式类似于 算法中的
算法中的 数组,只不过
数组,只不过 数组是求最长的两端一样的串,这道题我们要求最短的。
数组是求最长的两端一样的串,这道题我们要求最短的。
回想 中
中 数组的求法,我们每次按照最长的先匹配,这样如果当前加入的字符和
数组的求法,我们每次按照最长的先匹配,这样如果当前加入的字符和 位置的字符一样的话,就直接从上一个字符的
位置的字符一样的话,就直接从上一个字符的 直接扩展。如果失败的话,我们要通过
直接扩展。如果失败的话,我们要通过 数组跳到上一个肯定成功的位置的下一个,即
数组跳到上一个肯定成功的位置的下一个,即![j=next[j-1]+1](https://file.cfanz.cn/uploads/gif/2022/01/09/16/TM6c1B5482.gif) 。
。
通过这个思路,我们可以想到,如果我们想要求最短,那么一直用这种方式不断跳到最开始的位置,直到没有下一个位置可以跳了,就是最短的串的长度了。最后,我们要求的是前缀的长度,我们只需要用当前的串的长度减掉 的长度,就是当前字符串所求的长度了。最后将这些长度做和即可。
的长度,就是当前字符串所求的长度了。最后将这些长度做和即可。
AC代码
Codeforces Hello 2022
A - Stable Arrangement of Rooks
签到题。
B - Integers Shop
什么gb题面!一份礼物里可以有好多整数的吗原来!原来是把买的整数最小值和最大值之间的全送了……因为读错题面,苦苦思索+带着错误题面没读懂题解,浪费了两个半小时……
1.5
Codeforces Hello 2022
C - Hidden Permutations
简单交互题。从第一个开始,如果这个位置没确定,就一直询问这个位置,然后把给到的结果存起来,直到当前给到的数字和最开始是一样的就收手(说明已经到达一个循环了)。然后通过这一串数字,ans[a[j - 1]]=a[j]即可求出这些位置上的答案。然后查询下一个还没有答案的位置。
这个思路可以通过题目中的 启发出来,因为
启发出来,因为 的情况是1 2 3 4 5 ... n的最少询问次数。每次询问一个位置2次,发现两次输出的结果都一样,得出这个位置的答案。
的情况是1 2 3 4 5 ... n的最少询问次数。每次询问一个位置2次,发现两次输出的结果都一样,得出这个位置的答案。
D - The Winter Hike
右下角的 个格子的花费是不可避免的。只需要考虑移动的时候哪些点是必要的。由于移动次数没有限制,我们可以毛毛虫式的挪动。从左上角进到左下角,只用得上8个点:(1, n+1), (1, 2n), (n, n+1), (n, 2n), (n+1, 1), (n+1, n), (2n, 1), (2n, n)。我们只需要额外加上这八个点里面最小的花费即可。
个格子的花费是不可避免的。只需要考虑移动的时候哪些点是必要的。由于移动次数没有限制,我们可以毛毛虫式的挪动。从左上角进到左下角,只用得上8个点:(1, n+1), (1, 2n), (n, n+1), (n, 2n), (n+1, 1), (n+1, n), (2n, 1), (2n, n)。我们只需要额外加上这八个点里面最小的花费即可。
1.6
(刚买了两个月的电脑,硬件坏了,大无语。再加上身体上有些不适,看来最近不宜训练。渊下宫,香!)
Codeforces Round #756 (Div.3)
A - Make Even
答案只可能是-1,0,1,2。
AC代码
B - Team Composition: Programmers and Mathematicians
当 时,答案是
时,答案是 。
。
否则,假设 最大,考虑二者的差值,通过3 1的方式减少两者的差值,使其变成两个相等的数。因为可能还没减到相等,有一个就已经没了,所以要讨论原本最多可以减多少次和差值需要减多少次之间的大小关系。
最大,考虑二者的差值,通过3 1的方式减少两者的差值,使其变成两个相等的数。因为可能还没减到相等,有一个就已经没了,所以要讨论原本最多可以减多少次和差值需要减多少次之间的大小关系。
AC代码
C - Polycarp Recovers the Permutation
如果最后的结果,最左边或者最右边不是 ,那么这个结果是不可能出现的,因为
,那么这个结果是不可能出现的,因为 一定是最后入队的。
一定是最后入队的。
我们以 作为初始,维护一个双端队列,维护一个双指针
作为初始,维护一个双端队列,维护一个双指针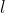 和
和 指向结果的左右端,比较左右端的值,如果左边的大,把这个数塞到双端队列的左端,然后令
指向结果的左右端,比较左右端的值,如果左边的大,把这个数塞到双端队列的左端,然后令 ;如果右边的大,把这个数塞到双端队列的右端,然后令
;如果右边的大,把这个数塞到双端队列的右端,然后令 。直到将所有的数全部入队之后,得到最初的排列,即为我们所求的答案。
。直到将所有的数全部入队之后,得到最初的排列,即为我们所求的答案。
AC代码
D - Weights Assignment For Tree Edges
根据树的形状,可以看出,子节点一定比父节点更晚被访问,可以按照题目要求的访问顺序,设距离分别为0,1,2,...,n-1,然后根据子父节点关系,![ans[son]=dist[son]-dist[parent]](https://file.cfanz.cn/uploads/gif/2022/01/09/16/Z6A2XIe1Ga.gif) 即可
即可 求得答案。
求得答案。
AC代码
1.7
身体不适,摸鱼。
1.8
依旧不宜训练
Nowcoder
25084 - [USACO 2006 Nov S]Bad Hair Day
单调栈大板子简单练习题。
(最后输出栈内剩余元素的答案时犯了老糊涂,导致WA了一发)
AC代码
15815 - Neat Tree
很巧妙的题目(对现在的我来说),感觉算是单调栈比较常用的用法。
计算所有区间的最大值与最小值的差,我们可以把问题简化成先求所有区间的最大值,再求所有区间的最小值,然后将所有区间的最大值和所有区间的最小值做差即可。
接下来看怎么求所有区间的最大值之和(所有区间的最小值之和同理):
数列中的每一个数对答案的贡献都是可求的,即设这个数在所有区间中,有 个区间里面这个数做了最大值,这个数的值是
个区间里面这个数做了最大值,这个数的值是 ,那么这个数对答案的贡献就是
,那么这个数对答案的贡献就是 。
。
现在我们来求这个 。这个数想做最大值,那么在对应区间中,这个数两侧的数一定都比它小。也就是说,假设左边第一个比这个数大的数字下标为
。这个数想做最大值,那么在对应区间中,这个数两侧的数一定都比它小。也就是说,假设左边第一个比这个数大的数字下标为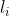 ,右边第一个比这个数大的数字下标为
,右边第一个比这个数大的数字下标为 ,那么我们可得
,那么我们可得 ,相当于左右边的可能长度枚举出来然后做一个组合。
,相当于左右边的可能长度枚举出来然后做一个组合。
但是我们如果用朴素方法来求,由于数据范围是 ,这样的
,这样的 做法肯定是不行的。
做法肯定是不行的。
我们考虑到,对于一个数,我们只需要考虑到左边第一个比它大的数,再往左边的数对它都没有任何作用,所以如果只维护从左边第一个比它大的数开始的序列,可以缩减它的时间。而这种做法,就是单调栈。求所有区间的最大值之和时,我们维护一个递减的单调栈。每当我们塞入一个数字时,这个数字弹到可能的最深的位置时,在栈中的前一个数,就是左边第一个比它大的数字。如果这个数被弹出去,那么令它被弹出去的那个数,就是右边第一个比它大的数字。
根据这样的性质,我们首先初始化所有的 ,
, 。然后走一遍单调栈,就可以获得所有数字左边和右边第一个比它大的数字的位置了。再通过上面的求法,就可以求得所有区间的最大值之和了。
。然后走一遍单调栈,就可以获得所有数字左边和右边第一个比它大的数字的位置了。再通过上面的求法,就可以求得所有区间的最大值之和了。
求所有区间的最小值之和的时候,只需要维护一个递增的单调栈即可。
最后结果就是所有区间的最大值之和-最小值之和。
AC代码
1.9
Nowcoder
20164 - 最大数MAXNUMBER
这道题目用线段树做简单无比,但是还是用单调栈写了一发。
可以发现,我们求后几位的最大值,也就是说,如果大数字越靠后,他越会成为更多所求范围的答案。假设倒数第1个数是50,是倒数四个数里面最大的;倒数第5个数是70,那么我们求后 个数中的最大值,那么当
个数中的最大值,那么当 时,答案都是50,而当
时,答案都是50,而当 时,答案就变成了70。而倒数第2,3,4个数中,由于倒数第一个数的加入,导致这三个数变得没有意义了,因为他们一定不会成为答案。所以我们可以尝试把他们抛弃,从而加快我们计算的速度。而这种思想和单调栈是一致的。
时,答案就变成了70。而倒数第2,3,4个数中,由于倒数第一个数的加入,导致这三个数变得没有意义了,因为他们一定不会成为答案。所以我们可以尝试把他们抛弃,从而加快我们计算的速度。而这种思想和单调栈是一致的。
那么我们如何计算倒数 个数里面最大的数值是多少呢?
个数里面最大的数值是多少呢?
考虑单调栈存储数值和数字下标的pair,我们的单调栈以数值排序,维护一个递减栈。当我们要插入数值时,我们记录当前插入数列末尾的数会是数列中的第几个数,并将其与数值合成一个pair,推入我们的单调栈中。
假设我们要求的是倒数 个数里面的最大值。我们只需要找单调栈里面下标为
个数里面的最大值。我们只需要找单调栈里面下标为 的值,那么那个数对对应的数值就是我们要求的答案。
的值,那么那个数对对应的数值就是我们要求的答案。
而我们发现,因为插入的顺序是固定的,所以单调栈中单调的不仅是数值,还有下标,下标也是单调递增的。所以直接二分查找下标值大于等于 的第一个数对的数值即可。
的第一个数对的数值即可。
AC代码










