【数据结构】八大排序（二）-CFANZ编程社区

前言：

前言：

冒泡排序

......

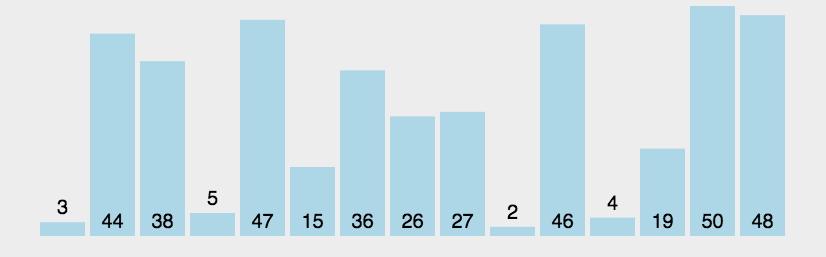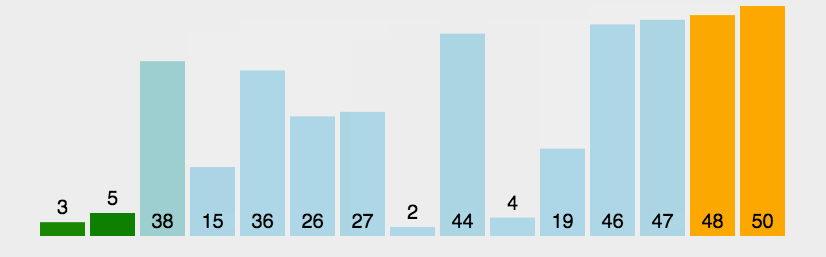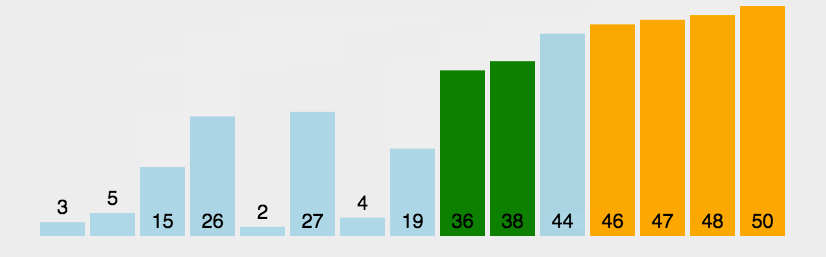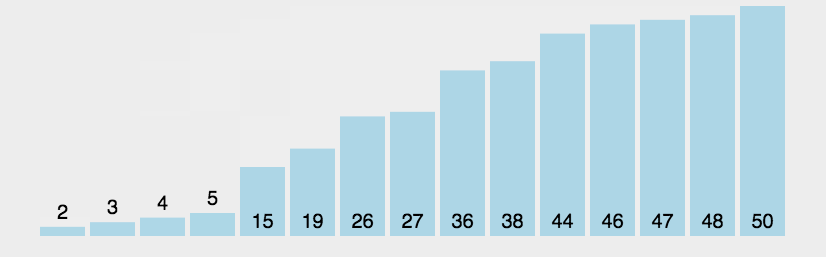
冒泡排序代码实现

void bubblesort(int arr[], int n)
{
	// 外层循环控制冒泡排序的趟数
	int i = 0;
	for (i = 0; i < n - 1; i++)
	{
		//内层循环控制要比较元素的个数
		int j = 0;
		for (j = 0; j < n - i - 1; j++)
		{
			int temp = 0;
			if (arr[j]>arr[j + 1])
			{
				temp = arr[j];
				arr[j] = arr[j + 1];
				arr[j + 1] = temp;
			}
		}
	}
}

冒泡排序特性总结

1.时间复杂度

2. 空间复杂度

3.算法稳定性

快速排序

单趟排序hoare版本

void swap(int* p, int* q)
{
	int tmp = *p;
	*p = *q;
	*q = tmp;
}
//单趟排序hoare版本
int PartSort(int* a, int left, int right)
{
	int keyi = left;//选取左边作为基准值，则右边先走
	while (left < right)//left与right相遇,左边找大，右边找小的循环终止
	{
        //右边找小
		while (left<right && a[right] >= a[keyi])
		{
			right--;
		}
        //左边找大
		while (left<right && a[left] <= a[keyi])
		{
			left++;
		}
        //交换
		swap(&a[left], &a[right]);

	}
	swap(&a[keyi], &a[left]);
	return left;
}

单趟排序挖坑法

//单趟排序挖坑法
int PartSort(int* a, int left, int right)
{
	int key = a[left];
	int hole = left;
	while (left < right)
	{
		//右边先走
		while (left < right && a[right] >= key)
		{
			right--;
		}
		a[hole]=a[right];
		hole = right;
		//左边再走
		while (left < right&&a[left] <= key)
		{
			left++;
		}
		a[hole] = a[left];
		hole = left;
	}

	a[hole] = key;
	return hole;
}

单趟排序快慢指针法

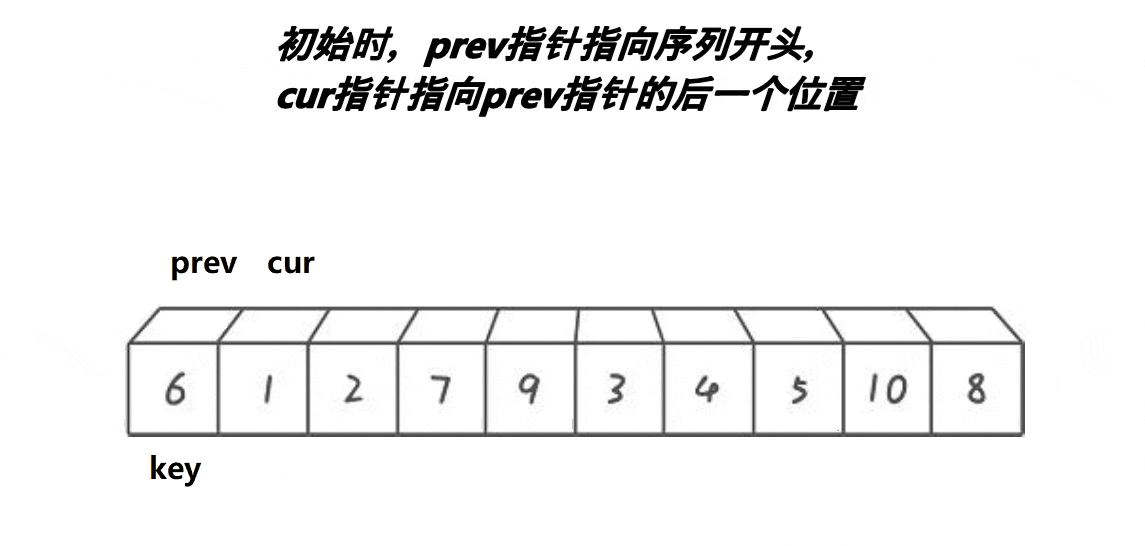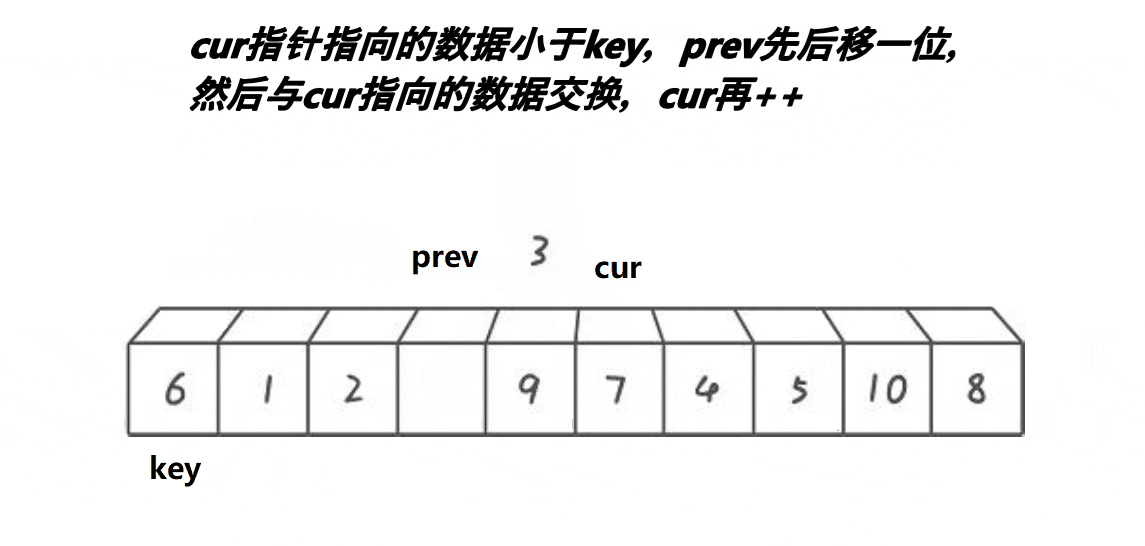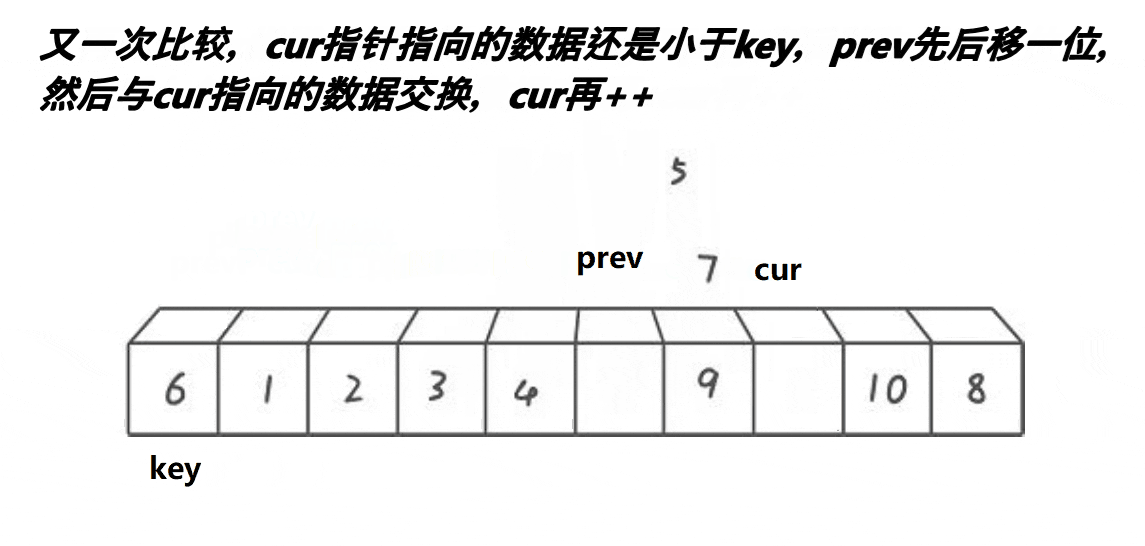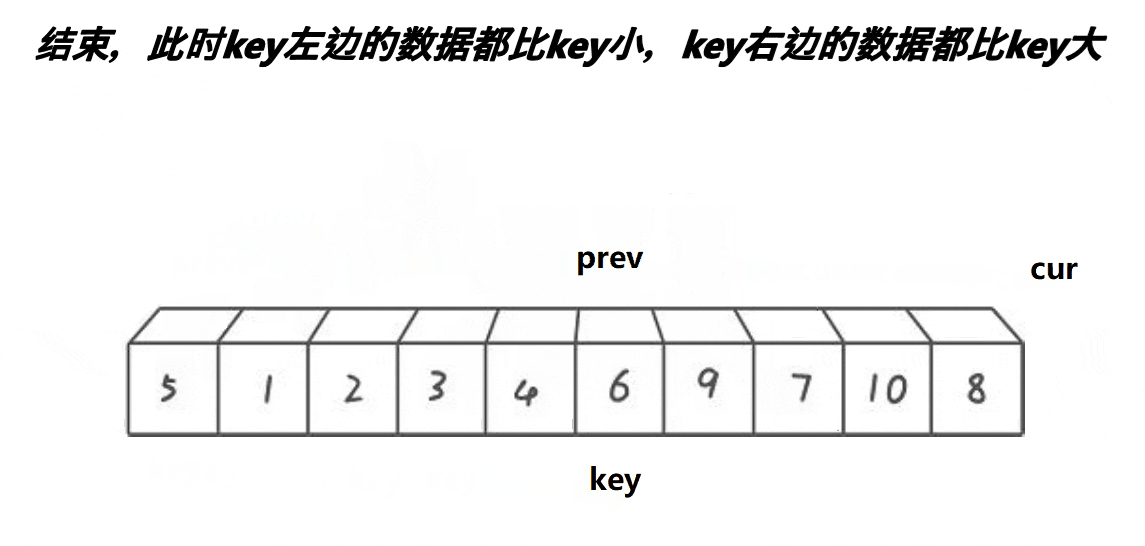
//单趟排序前后指针法
int PartSort(int* a, int left, int right)
{
	int keyi = left;
	int prev = left;
	int cur = prev + 1;
	while (cur <= right)
	{
		//(++prev)!=cur为了防止++prev与cur指向相同数值,此时交换毫无意义;
		if (a[cur] < a[keyi]&&(++prev)!=cur)
		{
			swap(&a[cur], &a[prev]);
		}
		cur++;
	}
	swap(&a[keyi], &a[prev]);
	return prev;
}

快速排序整体概览

快速排序首先选取基准值key，将待排序序列分为两个子序列，左子序列放比基准值小的数，右子序列放比基准值大的数，然后再将子序列以以上方式同样分割，直到数组有序，下图单趟排序采取hoare版本

经过一趟hoare排序，区间被划分为[begin, keyi-1] U keyi U [keyi+1, end] ，单趟排序一次就会唯一确定一个元素来到最终排序所确定的位置；

先递归排序左子序列[begin, keyi-1] , 再递归排序右子序列[keyi+1, end]，类似二叉树前序遍历；

根据上图可得出递归终止条件为区间不存在(begin>end)或者只有一个元素(begin=end)

void QuickSort(int*a, int begin, int end)
{
	//递归终止的条件
	//1.区间不存在(begin>end)或者只有一个元素(begin=end)
	if (begin >= end)
		return;
	int keyi = PartSort3(a, begin, end);
	// 一趟排序原排序区间划分为如下三部分
	//[begin keyi-1]U[keyi]U[keyi+1,end]
	QuickSort(a, begin, keyi - 1);
	QuickSort(a, keyi + 1, end);
}

快排的优化

三数取中法选key

//三数取中法选keyi keyi为中间值的下标
int GetMidi(int* a, int left, int right)
{
	int mid = (left + right) / 2;
	if (a[left] > a[mid])
	{
		if (a[mid] > a[right])
		{
			return mid;
		}
		//mid为最小值
		else if (a[left] > a[right])
		{
			return right;
		}
		else
		{
			return left;
		}
	}
	else
	{
		if (a[mid] < a[right])
		{
			return mid;
		}
		//mid为最大值
		else if (a[left]>a[right])
		{
			return left;
		}
		else
		{
			return right;
		}
	}
}

小区间优化

假设数组大小N=10，即二叉树节点个数N=10；

void QuickSort(int* a, int begin, int end)
{
	if (begin >= end)
		return;

	// 小区间优化，小区间不再递归分割排序，降低递归次数
	if ((end - begin + 1) > 10)
	{
		int keyi = PartSort(a, begin, end);

		// [begin, keyi-1] keyi [keyi+1, end]
		QuickSort1(a, begin, keyi - 1);
		QuickSort1(a, keyi + 1, end);
	}
	else
	{
		InsertSort(a + begin, end - begin + 1);
	}
}