递归
递归函数是函数体中直接或者间接调用自身的函数。
以 factorial 为例。
factorial 的递归实现如下:
def factorial(n):
if n == 0:
return 1
return n * factorial(n - 1)
从定义中可知 0!是 1,既然 n==0 是能计算阶乘的最小数字,可以用它当 基本情况(base case),递归部分也按照阶乘定义来,即,n! = n * (n-1)!
递归函数有3个重要部分:
-
base case。基本情况可以看作最简单的函数输入情况,或者当作递归停止条件。在上面的例子中,
factorial(1)是factorial的基本情况。 -
Recursive call on a smaller problem。你可以把这一步想成,对于当前问题所依赖的,在较小问题上的函数调用。并且假定这个较小问题上的递归调用会给我们预想的结果,称之为“递归的信仰之跃” (recursive leap of faith)。
-
Solve the larger problem。在第2步,我们找到了较小问题的解。我们现在想使用这个结果来弄清楚我们当前问题的解应该是什么,这就是我们想要从当前函数调用中返回的结果。在上面的例子中,我们可以通过将较小问题的解
factorial(n-1)(表示(n-1)!)乘以n来计算factorial(n)(因为n! = n * (n-1)!)。
本次实验中的问题将要求你编写递归函数。下面是一些通用提示:
- 比较矛盾的是,在函数编写完成之前,你需要假定该函数的功能已经完成;即所说的”递归的信仰之跃“。
- 思考如何利用更简单问题的解来解决当前问题。递归函数看似做的工作很少:记住要信仰之跃,要 相信递归 可以解决稍微小一点的问题,而不必担心它是如何解决的。
- 考虑最简单情况下的解是什么,这些就是基本情况 - 递归调用的停止点。请务必考虑是否遗漏了基本情况(这是递归失败的常见原因)。
- 首先编写迭代的版本可能会有所帮助。
树递归
树递归是不止调用一次自身的递归函数,产生一系列类似于树的调用。
例如,假设要递归计算 斐波那契数列的第 n 项,定义如下:
def fib(n):
if n == 0 or n == 1:
return n
return fib(n - 1) + fib(n - 2)
fib(6) 的调用结构看起来像一个倒置的树( f 是 fib):

每个 f(i)节点表示 表示对 fib的一次递归调用。每个 f(i) 递归调用都会再进行两个递归调用,即 f(i-1) 和 f(i-2)。每当到达 f(0) 或者 f(1)节点时,可以直接返回 0 或者 1 ,不再有更多的递归调用,因为这些是基本情况。
换句话说,基本情况可以直接返回答案所需的信息,而不依赖于其他递归调用的结果。一旦到达一个基本情况,就可以开始从递归到基本情况的递归调用返回。
一般来讲,树递归对于在当前状态下存在多种可能或者选择的问题比较有效。在这类问题中,你可以为每个选择或每组选择进行递归调用。
问题2:Line Stepper
完成函数 line_stepper ,该函数返回从 start 到 0 沿着数字线,每次走 k 步,到达 0 的路径数。注意每步 必须 要么向左或者向右,不能呆在原地!

例如,上面显示了从 3 开始走 5 步的所有可能路径。在每一步中,要么向左要么向右移动一步,并最终到达 0
def line_stepper(start, k):
"""
Complete the function line_stepper, which returns the number of ways there are to go from
start to 0 on the number line by taking exactly k steps along the number line.
>>> line_stepper(1, 1)
1
>>> line_stepper(0, 2)
2
>>> line_stepper(-3, 3)
1
>>> line_stepper(3, 5)
5
"""
"*** YOUR CODE HERE ***"
if start==0 and k==0:
return 1
if k<=0:
return 0
#向右走
right=line_stepper(start=start+1, k=k-1)
#向左走
left=line_stepper(start=start-1,k=k-1)
return right+left
编程问题
问题3:Summation
编写递归函数 summation, 接受一个正整数 n 和一个函数 term 。该函数将 term 应用到 1 到 n (包括 n)并返回和。
注意:使用递归;如果使用任何的循环(for, while),测试将失败。
def summation(n, term):
“”"Return the sum of numbers 1 through n (including n) wíth term applied to each number.
Implement using recursion!
>>> summation(5, lambda x: x * x * x) # 1^3 + 2^3 + 3^3 + 4^3 + 5^3
225
>>> summation(9, lambda x: x + 1) # 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10
54
>>> summation(5, lambda x: 2**x) # 2^1 + 2^2 + 2^3 + 2^4 + 2^5
62
>>> # Do not use while/for loops!
>>> from construct_check import check
>>> # ban iteration
>>> check(HW_SOURCE_FILE, 'summation',
... ['While', 'For'])
True
"""
assert n >= 1#检查函数,检查n的值是否大于1
"*** YOUR CODE HERE ***"
#if n==0:
# return 1
#return summation(n-1,term)+term(n)
x=1
def help(x):#使用帮助函数来避免assert 的检查
if x==n+1:
return 0
return help(x+1)+term(x)
return help(x)
使用 Ok 测试你的代码:
python3 ok --local -q summation
#### 问题4: Insect Combinatorics
考虑一只在 *M* x *N* 网格中的昆虫。昆虫从左下角 *(1, 1)* 开始(start),并希望最终在右上角*(M, N)* 结束(goal)。昆虫只能向右或向上移动。编写一个函数,该函数接受网格的长度和宽度,并返回昆虫从 start 到 goal 可以采取的不同路径数。(此问题有一个 [closed-form solution](https://en.wikipedia.org/wiki/Closed-form_expression),但请尝试使用递归回答。)
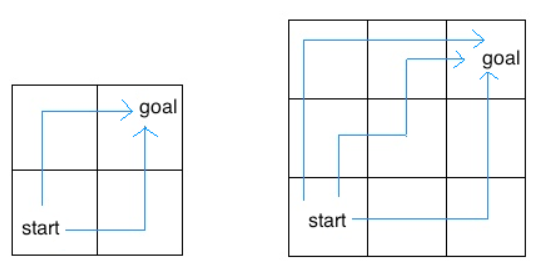
例如,2 x 2 网格总共有两种方式让昆虫从起点移动到目标。对于 3 x 3 网格,昆虫有 6 个不同的路径(上面只显示了 3 个)。
**提示**:如果碰到最顶端或最右边会发生什么?
```python
def paths(m, n):
"""Return the number of paths from one corner of an
M by N grid to the opposite corner.
>>> paths(2, 2)
2
>>> paths(5, 7)
210
>>> paths(117, 1)
1
>>> paths(1, 157)
1
"""
"*** YOUR CODE HERE ***"
if(m==1 ):
return 1
if(n==1):
return 1
if(m<0 or n<0):
return 0
if(m>0):
#向左走
x= paths(m-1,n)
#向下走
if(n>0):
y= paths(m,n-1)
return x+y
使用 Ok 测试你的代码:
python3 ok --local -q paths










