写在前面
学习二叉树结构,最简单的方式就是遍历。所谓二叉树遍历,就是按照某种特定的规则,一次对二叉树中的节点进行相应的操作,并且每个节点只操作一次。 访问节点所做的操作要看具体的应用问题。遍历是二叉树上最重要的运算之一,也是二叉树上进行其他运算的基础。
Ⅰ. BINARY TREE TRAVERSALS
0x00 概念
经常出现的一个操作是遍历树,也就是说,对树上的每个节点都精确访问一次。
完全遍历会对树中的信息产生一个线性顺序。
当遍历一棵树时,我们希望以同样的方式对待每个节点和它的子树。
假设对于树中的每个节点:
①
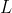
代表向左移动②

代表访问该节点(eg. 打印出数据字段)③

代表向右移动。
则存在 6 种可能的遍历组合:
—— 中序遍历(inorder traversal)
—— 后序遍历(postorder traversal)
—— 前序遍历(preorder traversal)
二叉树的三种遍历,与表达式的

三种形式,不乏紧密、自然的联系。

(图5.15)
0x01 中序遍历 - Inorder Traversal
void inorder(tree_pointer ptr)
/* inorder tree traversal */
{
if (ptr) {
inorder(ptr->left_child);
printf("%d", ptr->data);
inorder(ptr->right_child);
}
}
图5.15 按顺序输出:


0x02 前序遍历 - Preorder Traversal
void preorder(tree_pointer ptr)
/* preorder tree traversal */
{
if (ptr) {
printf("%d", ptr->data);
preorder(ptr->left_child);
preorder(ptr->right_child);
}
}
图5.15 按顺序输出:

0x03 后序遍历 - Postorder Traversal
void postorder(tree_pointer ptr)
/* postorder tree traversal */
{
if (ptr) {
postorder(ptr->left_child);
postorder(ptr->right_child);
printf("%d", ptr->data);
}
}
图5.15 按顺序输出:

0x04 非递归(循环)中序遍历 - Iterative Inorder Traversal
图5.16 含蓄地表现了 Program5.1 的堆叠和拆垛的过程。
一个没有动作的节点表示该节点被添加到堆栈中, - 而一个有printf动作的节点表示该节点被从堆栈中移除。 注意: - 左边的节点被堆叠起来,直到到达一个空节点, - 然后该节点被从堆叠中移除, - 该节点的右边子节点被堆叠起来
void iter_inorder(tree_pointer node)
{
int top = -1; /* initialize stack */
tree_pointer stack[MAX_STACK_SIZE];
for (; ; ) {
for (; node; node = node->left_child)
add(&top, node); /* add to stack */
node = delete(&top); /* delete from stack */
if (!node) break; /* empty stack */
printf("%d", node->data);
node = node->right_child;
}
}
🔑 iter_inorder 的分析:令

是树中结点个数。iterInorder 把每个节点入栈一次、出栈一次,所以时间复杂度为

,空间复杂度取决于树的深度,也是

。
0x05 层序遍历 - Level Order Traversal

📚 层序遍历(Level Traversal):设二叉树的根节点所在的层数为1的情况下,从二叉树的根节点出发,首先访问第1层的树根节点,然后再从左到右访问第2层上的节点。接着是第3层的节点……以此类推,自上而下、从左向右地逐层访问树的节点。
层序遍历需要利用队列来实现遍历。
void level_order(tree_pointer ptr)
/* level order tree traversal */
{
int front = rear = 0;
tree_pointer queue[MAX_QUEUE_SIZE];
if (!ptr) return; /* empty tree */
addq(front, &rear, ptr);
for (; ; ) {
ptr = deleteq(&front, rear); /*empty list returns NULL*/
if (ptr) {
printf("%d", ptr->data);
if (ptr->left_child)
addq(front, &rear, ptr->left_child);
if (ptr->right_child)
addq(front, &rear, ptr->right_child);
}
else break;
}
}
Ⅱ. 其他二叉树操作
0x00 复制二叉树
根据二叉树的定义,以及前中后序的递归实现,可以很容易地编写其他二叉树操作的C程序。
以常用的二叉树复制操作为例,程序 5.6 中的 copy 函数为实现代码。程序结构与刚才的 postorder 很接近,它实际上是根据它的代码修改而得到的,改动很少。
[Program 5.6] 复制二叉树
tree_pointer copy(tree_pointer original)
/* this function returns a tree_pointer to an exact copy
of the original tree */
{
tree_pointer temp;
if (original) {
temp = (tree_pointer)malloc(sizeof(node));
if (IS_FULL(temp)) {
fprintf(stderr, "The memory is full\n");
exit(1);
}
temp->left_child = copy(original->left_child);
temp->right_child = copy(original->right_child);
temp->data = original->data;
return temp;
}
return NULL;
}
0x01 判断两个二叉树全等 - Testing For Equality Of Binary Trees
两个全等的二叉树定义为两者的结构相等,并且对应数据域的内容相等。
int equal(tree_pointer first, tree_pointer second)
/* function returns FALSE if the binary trees first and
second are not equal, otherwise it returns TRUE */
{
return ((!first && !second) || (first && second &&
(first->data == second->data) &&
equal(first->left_child, second->left_child) &&
equal(first->right_child, second->right_child))
}
0x03 可满足性问题(The Satisfiability Problem)
考虑由遍历

和操作符

构成的演算公式集合。
变量只有两种取值 true 和 flase。
公式满足如下条件:

(1)一个变量是一个表达式
(2)如果 x 和 y 是表达式, 则

是表达式(3)操作符的优先级从高到低为

,但括号可以改变运算顺序。这三条基本规则可以生成命题演算的所有演算公式,如 "蕴含" 可用

表示。

对于给定的公式,是否存在一个变量集合的赋值,使该公式的求值结果为 true。
[program 5.8] 求解可满足性问题的第一个程序
for (all 2n possible combinations) {
generate the next combination;
replace the variables by their values;
evaluate the expression;
if (its value is true) {
printf(<combination>);
return;
}
}
printf("No satisfiable combination\n");<Evaluating an propositional formula>

为了评为了评估一个表达式,我们可以按后序遍历树,评估子树,直到整个表达式被简化为一个单一的值。 这对应于算术表达式的后缀评估。

[program 5.8] 后序求值
void post_order_eval(tree_pointer node)
{
/* modified postorder traversal to evaluate
a propositional calculus tree */
if (node) {
post_order_eval(node->left_child);
post_order_eval(node->right_child);
switch (node->data) {
case not : node->value =
!node->right_child->value;
break;
caseand : node->value =
node->right_child->value && node->left_child->value;
break;
case or : node->value =
node->right_child->value || node->left_child->value;
break;
case true: node->value = TRUE;
break;
case false: node->value = FALSE;
}
}
}
参考资料
Fundamentals of Data Structures in C










