戳一戳!和我一起走进深度学习的世界
导读
昨天我们讲解了卷积网络的基本概念和原理,卷积神经网络对于我们做视觉的人来说,是非常重要的工具,LeNet作为卷积神经网络的开篇,又能给我们带来什么样的体验呢?
今天要分享这篇文章带我们一起了解LeNet的基本原理,通过代码切实感受卷积神经网络的实现。让我们走进这篇文章,一起来了解一下吧!
如果你有什么问题,或者有什么想法,欢迎评论与我一起沟通交流。
本文目录
1 说在前面的话
2 LeNet-5 原理详解
A INPUT输入层
B C1卷积层
C S2池化层
D C3卷积层
E S4池化层
F C5卷积层-全连接层
G F6全连接层
H OUTPUT层-全连接层
3 LeNet代码实战
A 使用图片训练
B 使用图片编码训练
4 敲黑板
1 说在前面的话
A 温故知新
从这篇文章开始,我们就要深入了解卷积神经网络的模型了。
卷积神经网络是比较大块的内容了,应用范围也非常广泛,但是学习,我们要从基础开始。
在学习之前,我们先来回顾一下昨天讲的卷积神经网络的结构,神经网络主要有如下几层:
输入层,输入图像;
卷积层,提取图像特征;
ReLU层:对图像特征图做整流从而激活图像;
池化层,缩小图像尺寸,降低运算量;
全连接层,将所有特征图得到的特征联合进行识别。
但是我们要知道,一个真正的网络中,卷积层,ReLU层等会有好几层。
B LeNet-5
LeNet-5是LeCun在1998年提出的卷积神经网络,刚开始提出的时候,是为了解决手写数字识别的问题。

LeCun
LeNet是最基本的卷积神经网络算法,很多人也认为LeNet是卷积神经网络的开篇之作,LeNet也被当作卷积神经网络的雏形。有兴趣的同学,可以从这里,看一下原作,
http://vision.stanford.edu/cs598_spring07/papers/Lecun98.pdf
下面,我们就开始我们的原理讲解吧!
2 LeNet-5 原理详解
LeNet-5是比较简单的卷积神经网络,结构较为简单,一个完整的结构图如下:

LeNet-5的网络结构
我们就从每一层结构出发,去给大家讲述LeNet-5。
A INPUT输入层
我们昨天讲过卷积神经网络的第一层是输入层,也是最简单的一层,简单到有人认为它都不能算作一层。
在这里我们把它算作一层,因为输入层也很重要,我们要求输入图像的尺寸是32×32的图像。我们以单通道图像为例,也就是说,我们的图像为32×32×1的图像
B C1卷积层
上节课我们讲了卷积原理,讲了卷积神经网络中的卷积操作。
在LeNet网络中,卷积核的大小为5×5×1。卷积核每进行完一次卷积之后,还要再加上一个偏置量,然后,我们就会得到28×28×1的特征图,当我们使用六个卷积核对图像进行卷积操作,就会得到6个特征图,把这六个特征图合到一起,就是卷积层,卷积层的尺寸为28×28×6。
在这一层,同时也要使用激活函数处理,那为什么要使用激活函数呢?大家看下面这幅图:
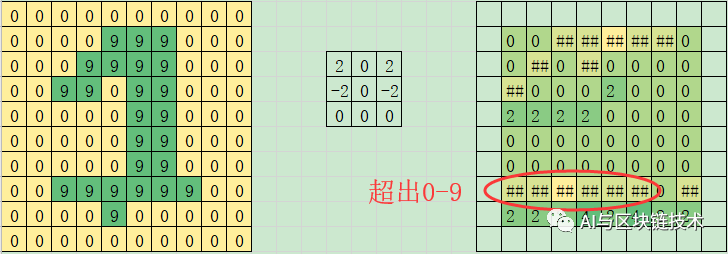
卷积后的结果
假设我们图像的像素范围是0-9。当我们使用卷积操作之后,我们会发现有的位置上的的值已经不在像素范围之内了。这在图像编码的时候是会出错的。那怎么办呢?
最简单的想法是,我们可以把大于9的统统改为9,小于0的统统改为0,这样,我们就能保证图像的像素在一个合法的范围内了。我们把这个想法用数学公式表示一下,就是下面这个公式:
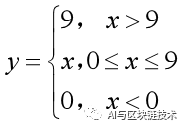
数学公式
这个公式对应的图是:
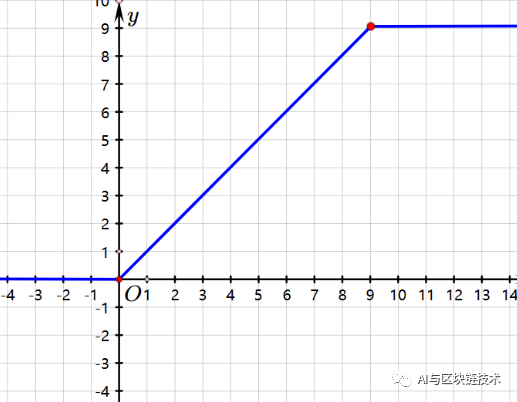
图像
这就是一个简单的激活函数,在LeNet中使用的激活函数是双曲正切函数:

双曲正切函数
通过激活函数计算之后,我们就能得到一个神经元,也就是说,一个神经元是感受野经过卷积核的卷积操作之后加上一个偏置量再进行激活后得到的一个像素位置,就是一个神经元。

神经元计算示意图
也就是说对于一个特征图来说,我们需要26个训练参数,其中有5×5=25个为卷积核,1个为偏置量。我们一共有六个特征图,也就是一共需要26×6=156个训练参数
总结一下,在卷积层中:
输入图片尺寸:32×32×1(也可以为32×32×3)
卷积核大小:5×5×1(也可以为5×5×3)
卷积核个数:6
特征图大小:28×28
神经元数量:28×28×6
训练参数个数:156(=(5×5+1)×6)
C S2池化层
这一层是池化层,将特征图的尺寸变为原来的1/4,在这里采用的是最大池化,即找区域为2×2正方形窗口中的最大值。经过池化操作后,特征图个数没有变化,只是每个特征图的大小变为了14×14的特征图。
总结一下,在池化层中:
输入特征图:28×28×6
池化窗口:2×2
池化方式:最大池化
输出特征图:14×14×6
D C3卷积层
和上面的卷积操作类似,但不同的是C3的每个节点与S2中的多个图相连。如下图所示:

C3的前6个特征图(对应上图第一个红框的6列)与S2层相连的3个特征图相连接(上图第一个红框),后面6个特征图与S2层相连的4个特征图相连接(上图第二个红框),后面3个特征图与S2层部分不相连的4个特征图相连接,最后一个与S2层的所有特征图相连。卷积核大小依然为5*5,所以总共有6*(3*5*5+1)+6*(4*5*5+1)+3*(4*5*5+1)+1*(6*5*5+1)=1516个参数。
举个例子:

C3与S2中前3个图相连
为什么要用这种方式呢?
主要有如下两方面的原因:
(1)将不同的特征图像卷积得到新的一个特征图,就可以把这几个特征图中的特征融合到一起。也能更好地做图像的识别。
(2)如果不这样,还按照前一个卷积层的操作方式,每一个新的特征图都由前面六个特征图得到,那一共需要(5×5×6+1)×16 = 2416个参数。这样的话,需要的参数太多,需要的连接数也太多,计算量就太大了,通过这种方式可以很好地降低计算量。
总结一下,在这一层的卷积层中:
输入特征图:14×14×6
卷积核大小:5×5
新特征图大小:10×10×16
训练参数个数:1516
E S4池化层
这一层是池化层,与上面的S2池化层的操作是一致的,只不过因为输入不同,所以输出也不同,同样将特征图的尺寸变为上一层的1/4,在这里采用的是最大池化,即找区域为2×2正方形窗口中的最大值。经过池化操作后,特征图个数没有变化,只是每个特征图的大小变为了5×5的特征图。
总结一下,在S4池化层中:
输入特征图:10×10×16
池化窗口:2×2
池化方式:最大池化
输出特征图:5×5×16
F C5卷积层-全连接层
这一次卷积跟前两次的卷积也依然有区别,但是跟前一次的最后一个卷积是一样的,就是将前一层的所有特征值全部卷积,然后加上偏置量进行激活,然后我们发现,因为特征图的尺寸是5×5的,卷积核也是5×5的,所以我们得到的是一个1×1的输出。然后我们使用120个卷积核,我们就可以得到120个特征图。因为上一层的深度是16,所以我们这一层采用的卷积核的深度也是16,也就是说我们卷积核的尺寸为:5×5×16,再加上一个偏置量,本层的可训练参数有 120×(5×5×16+1) = 48120 个。
这一层的网络结构如下:

C5的网络结构
因为这一层卷积的方式是全连接的方式,所有的都会参与到运算中, 这一层也算是全连接层。
总结一下,在C5卷积层中:
输入图像大小:5×5×16
卷积核大小:5×5×16
新特征图大小:1×1×120
训练参数个数:48120
G F6全连接层
在上一层,我们得到了一个尺寸为1×1×120的新特征图,在下一层,是我们所有要分类的图片,一共有84个,包括所有的数字,字母(英文大小写)和常见的标点符号:

84个字符类别
这一层的操作就是将120对应到84,用的是全连接。所以这一层是全连接层。具体操作为:将120个像素每个像素乘以它对应的权重再加上一个偏置量,经过激活函数处理后得到一个神经元,一共有84个神经元,所以这一层的训练参数和连接数为(120+1)×84=10164。
F6的网络结构如下:

F6的网络结构
总结一下,在F6全连接层中:
输入特征图:1×1×120
输出特征图:1×1×84
训练参数个数:10164
H Output层-全连接层
输出层由欧几里得径向基函数核(Euclidean Radial Basis Function, RBF)构成,具体如下:

其中xj表示上一层生成的向量,wij表示数字i对应的RBF应有的常向量,如果我们只考虑数字,那i的取值范围是从0-9,j的范围是0-83,RBF输出的值越接近于0,表示当前网络输入的识别结果与字符i越接近。每个核对应0-9中的一个类别。输出值最小的那个核对应的i就是这个模型识别出来的数字。
这一层的网络结构如下:

Output层的网络结构
这一层有84x10=840个参数和连接。
总结一下,在Output全连接层中:
输入大小:84×1
输出:物体的标签
训练参数个数:48120
3 LeNet 代码实战
讲完了原理,我们就来真真切切感受一下LeNet吧!在实战之前,大家需要先下载对应的数据集,大家可以加群326866692下载,所有代码也会上传到群里,群里也有很多机器学习,深度学习有关的资料免费分享:

如果你使用图片数据集,就要使用第一段代码,如果你使用编码的数据集,就要使用第二段代码
有了数据集之后,我们开始吧!
我们用python和TensorFlow来完成我们的代码,这是因为,有很多小功能,可以用TensorFlow帮我们解决,我们就可以把大部分精力放在模型本身上,也能更能好的理解模型。
我们新建一个项目,LeNet,然后将数据集解压到这个文件夹中来,注意是整个文件夹解压进来,而不是压缩文件。

通过上面的原理讲解,我们知道,我们的流程如下:
1.输入并加载图像
2.定义模型
3.训练参数设置
4.使用模型进行训练
5.模型测试
A 使用图片训练
使用图片训练模型时,我们需要下载一个包:scikit-image,这样我们才能在代码中引用skimage,引用这个包的目的是为了更好地加载图像。
1.输入并加载图像
为了方便,我们定义一个函数来读取图片:
def read_image(path):
'''
读取图像
:param path: 图像路径,相对路径
:return:
'''
label_dir = [path+x for x in os.listdir(path) if os.path.isdir(path+x)]
images = []
labels = [] for index,folder in enumerate(label_dir): for img in glob.glob(folder+'/*.png'): # print("reading the image:%s"%img)
image = io.imread(img)
image = transform.resize(image,(32,32,1))
images.append(image)
labels.append(index) return np.asarray(images,dtype=np.float32),np.asarray(labels,dtype=np.int32)
然后我们加载模型并简单设置:
'''数据加载'''
train_path = "mnist/train/"
test_path = "mnist/test/"
#读取训练数据及测试数据
train_data,train_label = read_image(train_path)
test_data,test_label = read_image(test_path)
#乱序
train_image_num = len(train_data)
train_image_index = np.arange(train_image_num)
np.random.shuffle(train_image_index)
train_data = train_data[train_image_index]
train_label = train_label[train_image_index]
test_image_num = len(test_data)
test_image_index = np.arange(test_image_num)
np.random.shuffle(test_image_index)
test_data = test_data[test_image_index]
test_label = test_label[test_image_index]
x = tf.placeholder(tf.float32,[None,32,32,1],name='x')
y_ = tf.placeholder(tf.int32,[None],name='y_')
2.定义模型
然后我们需要定义7层模型:
def LeNet_syx(input_tensor,train,regularizer):
'''
LeNet函数
:param input_tensor: 输入张量
:param train:
:param regularizer:
:return:
'''
#第一层:卷积层,过滤器的尺寸为5×5,深度为6,不使用全0补充,步长为1。
#尺寸变化:32×32×1->28×28×6
with tf.variable_scope('layer1-conv1'):
conv1_weights = tf.get_variable('weight',[5,5,1,6],initializer=tf.truncated_normal_initializer(stddev=0.1))
conv1_biases = tf.get_variable('bias',[6],initializer=tf.constant_initializer(0.0))
conv1 = tf.nn.conv2d(input_tensor,conv1_weights,strides=[1,1,1,1],padding='VALID')
relu1 = tf.nn.relu(tf.nn.bias_add(conv1,conv1_biases))
#第二层:池化层,过滤器的尺寸为2×2,使用全0补充,步长为2。
#尺寸变化:28×28×6->14×14×6
with tf.name_scope('layer2-pool1'):
pool1 = tf.nn.max_pool(relu1,ksize=[1,2,2,1],strides=[1,2,2,1],padding='SAME')
#第三层:卷积层,过滤器的尺寸为5×5,深度为16,不使用全0补充,步长为1。
#尺寸变化:14×14×6->10×10×16
with tf.variable_scope('layer3-conv2'):
conv2_weights = tf.get_variable('weight',[5,5,6,16],initializer=tf.truncated_normal_initializer(stddev=0.1))
conv2_biases = tf.get_variable('bias',[16],initializer=tf.constant_initializer(0.0))
conv2 = tf.nn.conv2d(pool1,conv2_weights,strides=[1,1,1,1],padding='VALID')
relu2 = tf.nn.relu(tf.nn.bias_add(conv2,conv2_biases))
#第四层:池化层,过滤器的尺寸为2×2,使用全0补充,步长为2。
#尺寸变化:10×10×6->5×5×16
with tf.variable_scope('layer4-pool2'):
pool2 = tf.nn.max_pool(relu2,ksize=[1,2,2,1],strides=[1,2,2,1],padding='SAME')
#将第四层池化层的输出转化为第五层全连接层的输入格式。第四层的输出为5×5×16的矩阵,然而第五层全连接层需要的输入格式
#为向量,所以我们需要把代表每张图片的尺寸为5×5×16的矩阵拉直成一个长度为5×5×16的向量。
#举例说,每次训练64张图片,那么第四层池化层的输出的size为(64,5,5,16),拉直为向量,nodes=5×5×16=400,尺寸size变为(64,400)
pool_shape = pool2.get_shape().as_list()
nodes = pool_shape[1]*pool_shape[2]*pool_shape[3]
reshaped = tf.reshape(pool2,[-1,nodes])
#第五层:全连接层,nodes=5×5×16=400,400->120的全连接
#尺寸变化:比如一组训练样本为64,那么尺寸变化为64×400->64×120
#训练时,引入dropout,dropout在训练时会随机将部分节点的输出改为0,dropout可以避免过拟合问题。
#这和模型越简单越不容易过拟合思想一致,和正则化限制权重的大小,使得模型不能任意拟合训练数据中的随机噪声,以此达到避免过拟合思想一致。
#本文最后训练时没有采用dropout,dropout项传入参数设置成了False,因为训练和测试写在了一起没有分离,不过大家可以尝试。
with tf.variable_scope('layer5-fc1'):
fc1_weights = tf.get_variable('weight',[nodes,120],initializer=tf.truncated_normal_initializer(stddev=0.1))
if regularizer != None:
tf.add_to_collection('losses',regularizer(fc1_weights))
fc1_biases = tf.get_variable('bias',[120],initializer=tf.constant_initializer(0.1))
fc1 = tf.nn.relu(tf.matmul(reshaped,fc1_weights) + fc1_biases)
if train:
fc1 = tf.nn.dropout(fc1,0.5)
#第六层:全连接层,120->84的全连接
#尺寸变化:比如一组训练样本为64,那么尺寸变化为64×120->64×84
with tf.variable_scope('layer6-fc2'):
fc2_weights = tf.get_variable('weight',[120,84],initializer=tf.truncated_normal_initializer(stddev=0.1))
if regularizer != None:
tf.add_to_collection('losses',regularizer(fc2_weights))
fc2_biases = tf.get_variable('bias',[84],initializer=tf.truncated_normal_initializer(stddev=0.1))
fc2 = tf.nn.relu(tf.matmul(fc1,fc2_weights) + fc2_biases)
if train:
fc2 = tf.nn.dropout(fc2,0.5)
#第七层:全连接层(近似表示),84->10的全连接
#尺寸变化:比如一组训练样本为64,那么尺寸变化为64×84->64×10。最后,64×10的矩阵经过softmax之后就得出了64张图片分类于每种数字的概率,即得到最后的分类结果。
with tf.variable_scope('layer7-fc3'):
fc3_weights = tf.get_variable('weight',[84,10],initializer=tf.truncated_normal_initializer(stddev=0.1))
if regularizer != None:
tf.add_to_collection('losses',regularizer(fc3_weights))
fc3_biases = tf.get_variable('bias',[10],initializer=tf.truncated_normal_initializer(stddev=0.1))
logit = tf.matmul(fc2,fc3_weights) + fc3_biases
return logit
3.训练参数设置
定义好模型后,我们就能按照我们上面讲解的,根据模型设置训练相关参数:
'''训练参数设置'''
regularizer = tf.contrib.layers.l2_regularizer(0.001)
y = LeNet_syx(x,False,regularizer)
cross_entropy = tf.nn.sparse_softmax_cross_entropy_with_logits(logits=y,labels=y_)
cross_entropy_mean = tf.reduce_mean(cross_entropy)
loss = cross_entropy_mean + tf.add_n(tf.get_collection('losses'))
train_op = tf.train.AdamOptimizer(0.001).minimize(loss)
correct_prediction = tf.equal(tf.cast(tf.argmax(y,1),tf.int32),y_)
accuracy = tf.reduce_mean(tf.cast(correct_prediction,tf.float32))
4.训练
使用训练参数训练模型:
'''训练过程'''
#每次获取batch_size个样本进行训练或测试
def get_batch(data,label,batch_size):
for start_index in range(0,len(data)-batch_size+1,batch_size):
slice_index = slice(start_index,start_index+batch_size)
yield data[slice_index],label[slice_index]
#创建Session会话
with tf.Session() as sess:
#初始化所有变量(权值,偏置等)
sess.run(tf.global_variables_initializer())
sample_num = 10
batch_size = 64
for i in range(sample_num):
train_loss,train_acc,batch_num = 0, 0, 0
for train_data_batch,train_label_batch in get_batch(train_data,train_label,batch_size):
_,err,acc = sess.run([train_op,loss,accuracy],feed_dict={x:train_data_batch,y_:train_label_batch})
train_loss+=err;train_acc+=acc;batch_num+=1
print("train loss:",train_loss/batch_num)
print("train acc:",train_acc/batch_num)
train loss: 0.42046549951254114
train acc: 0.9141708911419424
train loss: 0.1774476085935611
train acc: 0.9746197972251868
train loss: 0.13331644760251934
train acc: 0.9811065901814301
train loss: 0.10787666700343057
train acc: 0.9845250800426895
train loss: 0.09339438358932066
train acc: 0.9868096318036286
train loss: 0.08440000619918203
train acc: 0.987726787620064
train loss: 0.0774204385612983
train acc: 0.9888273745997865
train loss: 0.07225998248527246
train acc: 0.9899779882604055
train loss: 0.0684412972148798
train acc: 0.9907784151547492
train loss: 0.06556981873152859
train acc: 0.9912119797225186
5.模型测试
训练好模型后,我们可以测试一下我们训练好的模型:
#创建Session会话with tf.Session() as sess: #初始化所有变量(权值,偏置等)
sess.run(tf.global_variables_initializer())
sample_num = 10
batch_size = 64
for i in range(sample_num):
test_loss,test_acc,batch_num = 0, 0, 0
for test_data_batch,test_label_batch in get_batch(test_data,test_label,batch_size):
err,acc = sess.run([loss,accuracy],feed_dict={x:test_data_batch,y_:test_label_batch})
test_loss+=err;test_acc+=acc;batch_num+=1
print("test loss:",test_loss/batch_num)
print("test acc:",test_acc/batch_num)
测试结果如下:
test loss: 0.20972381847409102
test acc: 0.9700520833333334
test loss: 0.15120210374395052
test acc: 0.9774639423076923
test loss: 0.12053242005789891
test acc: 0.9819711538461539
test loss: 0.10226807189293396
test acc: 0.9841746794871795
test loss: 0.09191050612105009
test acc: 0.9866786858974359
test loss: 0.08625063429085109
test acc: 0.9866786858974359
test loss: 0.0856992670884117
test acc: 0.9860777243589743
test loss: 0.08331315849836056
test acc: 0.9867788461538461
test loss: 0.08433258614670007
test acc: 0.9860777243589743
test loss: 0.0832502302976373
test acc: 0.9859775641025641
B 使用图片编码进行训练
使用图片编码训练时,我们采用不同的方式。这里我们要注意一个问题,就是图片编码的尺寸是28×28的,但这并不影响我们进行模型训练,只是可能在模型中的设置跟我们上面讲到的不太一样,但是,原理是完全一致的。为了方便后面的代码,我们先定义几个函数:
'''函数定义'''
def showImage(image_data, k):
'''
图像格式输出
:param image_data: 输入图像
:return:
'''
plt.figure()
im = image_data[k].reshape(28, 28)
plt.imshow(im,'gray')
plt.pause(0.0000001)
def conv_kernel(shape):
"""
生成卷积核
:param shape: 卷积核的尺寸,四元组,前两个表示卷积核的行和列,第三个表示卷积核的深度,第四个表示卷积核的个数
:return: 初始随机化的卷积核
"""
initial = tf.truncated_normal(shape, stddev=0.1) #生成正态分布数据,标准差为0.1
return tf.Variable(initial)
def bias(shape):
"""
生成偏置量
:param shape: 偏置量的尺寸,一元组,每个特征图的偏置量,等于当前层卷积核的个数
:return: 初始随机化的偏置量
"""
initial = tf.constant(0.1, shape=shape)
return tf.Variable(initial)
def conv2d(image, ck):
"""
进行卷积操作
:param image: 输入图像
:param ck: conv kernel 卷积核
:param pad: 边框样式,可取值为:'SAME' (使用全0补充) 和 'VALID' (不使用全0补充)
:return:图像卷积操作后的值
"""
return tf.nn.conv2d(input=image, filter=ck, strides=[1, 1, 1, 1], padding='SAME')
def max_pool_2x2(image):
"""
最大池化
:param image: 输入图像
:return: 池化后的图像
"""
return tf.nn.max_pool(image, ksize=[1, 2, 2, 1], strides=[1, 2, 2, 1], padding='SAME')
1.输入并加载图像
我们定义一个专门的包来获取数据:
# coding=utf-8
import tensorflow as tf
from tensorflow.examples.tutorials.mnist
import input_data
import matplotlib.pyplot as plt
'''获得数据集'''
def get_data_syx():
return input_data.read_data_sets("MNIST_data/", one_hot=True);
然后在我们的训练代码中调用,并进行一些设置:
'''数据加载'''
mnist = getData.get_data_syx()
sess = tf.InteractiveSession()
x = tf.placeholder('float', shape=[None, 28*28])
y_true = tf.placeholder('float', shape=[None, 10])
x_image = tf.reshape(x, [-1, 28, 28, 1]) #将tensor变换为参数shape形式
2.定义模型
然后我们需要定义7层模型,上面已经定义了相关的函数,我们在这里直接使用就行:
'''结构定义'''
# C1卷积层
ck1 = conv_kernel([5, 5, 1, 6]) # 卷积核,权重参数
b1 = bias([6]) # 偏置量
r1 = tf.nn.relu(conv2d(x_image, ck1) + b1) # 激活函数 28
# S2池化层
p2 = max_pool_2x2(r1) #14
# C3卷积层
ck3 = conv_kernel([5, 5, 6, 16])
b3 = bias([16])
r3 = tf.nn.relu(conv2d(p2, ck3) + b3) #14
# S4 池化层
p4 = max_pool_2x2(r3) #14
p4_new = tf.reshape(p4, [-1, 7 * 7 * 16])
# C5 卷积-全连接层
ck5 = conv_kernel([7 * 7 * 16, 120])
b5 = bias([120])
r5 = tf.nn.relu(tf.matmul(p4_new, ck5) + b5)
# F6 全连接层
ck6 = conv_kernel([120, 84])
b6 = bias([84])
r6 = tf.nn.relu(tf.matmul(r5, ck6) + b6)
# Output层
ck7 = conv_kernel([84, 10])
b7 = bias([10])
sm7 = tf.nn.softmax(tf.matmul(r6, ck7) + b7) # softmax逻辑回归,将输入映射为0-1之间的实数。
3.训练参数设置
定义好模型后,我们就可以初始化我们的训练参数:
'''训练参数设置'''
cross_entropy = -tf.reduce_sum(y_true*tf.log(sm7))
train_step = tf.train.AdamOptimizer(1e-3).minimize(cross_entropy)
correct_prediction = tf.equal(tf.argmax(sm7, 1), tf.argmax(y_true, 1))
accuracy = tf.reduce_mean(tf.cast(correct_prediction, 'float'))
4.训练
使用训练参数训练模型:
'''训练过程'''
# 初始化所有变量(权值,偏置等)
sess.run(tf.global_variables_initializer())
for i in range(1000):
batch = mnist.train.next_batch(60)
if i%100 == 0:
train_accuracy = accuracy.eval(session=sess, feed_dict={x: batch[0], y_true: batch[1]})
print('step {}, training accuracy: {}'.format(i, train_accuracy))
train_step.run(session=sess, feed_dict={x: batch[0], y_true: batch[1]})
训练过程的中间结果如下:
step 0, training accuracy: 0.10000000149011612
step 100, training accuracy: 0.9166666865348816
step 200, training accuracy: 0.949999988079071
step 300, training accuracy: 0.9166666865348816
step 400, training accuracy: 0.9666666388511658
step 500, training accuracy: 0.9666666388511658
step 600, training accuracy: 0.9666666388511658
step 700, training accuracy: 0.9666666388511658
step 800, training accuracy: 1.0
step 900, training accuracy: 0.9666666388511658
5.模型测试
训练好模型后,我们可以测试一下我们训练好的模型:
'''结果测试'''
print('test accuracy: {}'.format(accuracy.eval(session=sess, feed_dict={x: mnist.test.images, y_true: mnist.test.labels})))
测试结果如下:
test accuracy: 0.9787999987602234
4 敲黑板
LeNet-5原理及相关参数。(重点)
LeNet-5代码实战。
注:敲黑板是对这篇文章重点的简要总结,大家可以在下面评论留言自己的学习笔记,学习感悟。











