【机器学习】逻辑回归-CFANZ编程社区

上一篇：【机器学习】线性回归（超详细）

逻辑回归属于监督学习里的分类问题，所谓“分类”，指的是：因变量y取值为离散的情况，一般取值为0或1.这决定了逻辑回归算法中的一个比较重要的性质：它的输出值永远在0到1之间。所以，我们的假设函数就不能和线性回归的假设函数一样，而需要重新定义。

逻辑回归的假设函数

逻辑回归的假设函数： $h_{\theta }(x)=g(\theta ^{T}x)=g(z)=\frac{1}{1+e^{-z}}=\frac{1}{1+e^{-\theta ^{T}x}}$

对模型的理解： $g(z)=\frac{1}{1+e^{-z}}$

例如，对于给定的x，通过已知的参数计算出 $h_{\theta }=0.7$ ,则表示有70%的概率y为1.

决策边界

我们对决策边界概念的理解能够更好的帮助我们理解逻辑回归的假设函数在计算什么。下面讲决策边界的概念：

在逻辑回归中，我们预测：

当 $h_{\theta }(x)>=0.5$ 时，预测y=1.

当 $h_{\theta }(x)<0.5$ 时，预测y=0.

根据上面绘制的图像，我们知道：

当z>=0时，g(z)>=0.5

当z<0时，g(z)<0.5

又因为 $z=\theta ^{T}x$ ,即

举个例子：

大于这条线的部分预测y=0,小于这条线的部分预测y=0. 这条线就叫做决策边界。

代价函数

对于线性回归，我们知道它的代价函数为： $J(\theta )=\frac{1}{2m}\Sigma _{i=1}^{m}(h_{\theta }x^{(i)}-y^{(i)})^{2}$ ,我们可以对其进行梯度下降求最小值。其中可以用梯度下降最根本的原因在于它是一个凸函数，如下图所示

在逻辑回归中，如果还用和线性回归一样的代价函数的话，是求不到全局的最小值的，只能求到局部的最小值。这是因为，逻辑回归的假设函数变成了 $h_{\theta }(x)=g(\theta ^{T}x)=g(z)=\frac{1}{1+e^{-z}}=\frac{1}{1+e^{-\theta ^{T}x}}$ 。将其带入 $J(\theta )=\frac{1}{2m}\Sigma _{i=1}^{m}(h_{\theta }x^{(i)}-y^{(i)})^{2}$ 可得到它的图像为:

由此我们知道，我们需要重新定义逻辑回归的代价函数。且这个代价函数一定是一个凸函数。

所以，逻辑回归的代价函数有如下定义： $J(\theta )=\frac{1}{m}\Sigma _{i=1}^{m}cost(h_{\theta }(x^{(i)}),y^{(i)})$

这样构建 $cost(h_{\theta }(x^{(i)}),y^{(i)})$ 函数的特点是：当实际的 𝑦 = 1 且ℎ𝜃(𝑥)也为 1 时误差为 0，当 𝑦 = 1 但ℎ𝜃(𝑥)不为 1 时误差随着ℎ𝜃(𝑥)变小而变大；当实际的 𝑦 = 0 且ℎ𝜃(𝑥)也为 0 时代价为 0，当𝑦 = 0 但ℎ𝜃(𝑥)不为 0 时误差随着 ℎ𝜃(𝑥)的变大而变大。

在得到这样一个代价函数以后，我们便可以用梯度下降法来求得代价函数取最小值时的参数了。算法为：

注：虽然得到的梯度下降算法表面上看上去与线性回归的梯度下降算法一样，但是这里的ℎ 𝜃 (𝑥) = 𝑔(𝜃 𝑇 𝑋) 与线性回归中不同，所以实际上是不一样的。另外，在运行梯度下降算法之前，进行特征缩放依旧是非常必要的。

正则化

正则化的思路：尽量减少参数 $\theta$ 的值。

正则化的目的：改善或减少过度拟合的问题。

下面介绍什么是过拟合问题。

过拟合的问题

到现在为止，我们学习了线性回归和逻辑回归，但是在应用过程中，可能会遇到过拟合问题，导致它们解决问题的效果很差。那么什么是过拟合？

下面是一个回归问题的例子：

第一个模型很明显是欠拟合，即不能很好的适应我们的数据。第三个模型虽然能够很好的拟合原始数据（训练集），但是它却不能很好的拟合测试集，若给出一个新的值让它预测的话，它将预测的很差。而中间的模型则是最适合的，既能很好的拟合原始数据，又能很好的预测新的数据。

同样的，分类问题也存在这样的问题：

问题是，如果我们发现了过拟合问题，应该如何处理？

1. 丢弃一些不能帮助我们正确预测的特征。可以是手工选择保留哪些特征，或者使用一些模型选择的算法来帮忙（例如 PCA ）。

2. 正则化。保留所有的特征，但是减少参数的大小（ magnitude ）。

正则化之后的代价函数

我们可以从之前的示例中看出，正是由于那些高次项导致了过拟合的产生。所以，如果我们能够让那些高次项系数接近于0的话，我们就能够很好的拟合了。但是往往在实际问题中，我们并不知道哪些参数是高次项的系数，于是，我们便将所有的参数进行减小。所以我们要做的是在一定程度上减少所有 $\theta$ 的值，这就正则化的基本方法。

那么为什么增加一项 $\lambda \Sigma _{j=1}^{n}\theta _{j}^{2}$ ,就可以使 $\theta$ 变小呢？

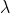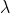因为如果我们令 $\lambda$ 值很大的话，为了使代价函数的值尽可能的减小，所有的 $\theta$ 值都会在一定程度上减小（不包括 $\theta _{0}$ ）。但是 $\lambda$ 值太大的话，那么 $\theta$ （不包括 $\theta _{0}$ ）都会趋向于0，这样我们得到的只能是平行于x轴的直线。