基于ldap实现登录认证

目录

直接插入排序

希尔排序

选择排序

冒泡排序

堆排序 

快速排序

hoare法

挖坑法

 前后指针法

 非递归版本

 快速排序中的优化

归并排序

递归版本

非递归版本

计数排序

 总结

直接插入排序

动图演示

代码实现： 

//直接插入排序—时间复杂度O(N^2)
void InsertSort(vector<int> &v, int n)
{
	//end只用到n-2位置即可
	for (int i = 0; i < n - 1; i++)
	{
		int end = i;
		int tmp = v[end + 1];
		while (end >= 0)
		{
			if (tmp < v[end])
			{
				v[end + 1] = v[end];
				end--;
			}
			else
			{
				break;
			}
		}
		v[end + 1] = tmp;
	}
}

希尔排序

代码实现： 

//希尔排序
void ShellSort(vector<int>& v, int n)
{
	//gap > 1时是预排序
	//gap == 1时直接插入排序
	int gap = n;
	while (gap > 1)
	{
		gap = gap / 3 + 1;
		for (int i = 0; i < n - gap; i++)
		{
			int end = i;
			int tmp = v[end + gap];
			while (end >= 0)
			{
				if (tmp < v[end])
				{
					v[end + gap] = v[end];
					end -= gap;
				}
				else
				{
					break;
				}
			}
			v[end + gap] = tmp;
		}
	}
}

选择排序

动图演示

代码实现： 

代码上小优化，可以同时找最大和最小的数，使得排序更快

//选择排序—时间复杂度O(N^2)
void SelectSort(vector<int>& v, int n)
{
	int begin = 0, end = n - 1;
	int mini = begin, maxi = begin;
	while (begin < end)
	{
		for (int i = begin + 1; i < end; i++)
		{
			//找小的数
			if (v[i] < v[mini])
				mini = i;

			//找大的数
			if (v[i] > v[maxi])
				maxi = i;
		}
		Swap(v[begin], v[mini]);

		//如果begin和maxi重叠，那么需要修正maxi
		if (begin == maxi)
		{
			maxi = mini;
		}

		Swap(v[end], v[maxi]);
		begin++;
		end--;
	}
}

 冒泡排序

 动图演示

代码实现： 

//冒泡排序—时间复杂度O(N^2)
void BubbleSort(vector<int>& v, int n)
{
	for (int i = 0; i < n; i++)
	{
		int exchange = 0;
		for (int j = 1; j < n - i; j++)
		{
			if (v[j - 1] > v[j])
			{
				Swap(v[j - 1], v[j]);
				exchange = 1;
			}
		}
		if (exchange == 0)
		{
			break;
		}
	}
}

堆排序 

 代码实现： 

//堆排序—建大根堆
void AdjustDown(vector<int> &v, int n, int root)
{
	int child = root * 2 + 1;
	while (child < n)
	{
		//选出左右孩子中大的那个
		if (child + 1 < n && v[child + 1] > v[child])//防止数组越界
		{
			child++;
		}
		//孩子和父亲比较
		if (v[child] > v[root])
		{
			Swap(v[child], v[root]);
			root = child;
			child = root * 2 + 1;
		}
		else
		{
			break;
		}
	}
}

void HeapSort(vector<int>& v, int n)
{
	for (int i = (n - 1 - 1 ) / 2; i >= 0; i--)
	{
		AdjustDown(v, n, i);//向下调整前提：左右子树必须是大/小堆
	}
	// o(N*logN)
	int end = n - 1;
	while (end > 0)
	{
		Swap(v[0], v[end]);
		AdjustDown(v, end, 0);
		end--;
	}
}

 快速排序

要实现快速排序可以有以下几种方法：

hoare法

代码实现： 

void QuickSort(vector<int>& v, int begin, int end)
{
	//如果只剩一个值或者区间不存在直接返回
	if (begin >= end)
	{
		return;
	}

	int left = begin, right = end;
	int keyi = left;
	while (left < right)
	{
		//右边先走，找到比key小的就停下来
		while (left < right && v[right] >= v[keyi])
		{
			right--;
		}

		//左边走，找到比key大的就停下来
		while (left < right && v[left] <= v[keyi])
		{
			left++;
		}

		Swap(v[left], v[right]);
	}
	Swap(v[keyi], v[left]);
	keyi = left;
	//左区间
	QuickSort(v, begin, keyi - 1);
	//右区间
	QuickSort(v, keyi + 1, end);
}

挖坑法

代码实现： 

void QuickSort(vector<int>& v, int begin, int end)
{
	//如果只剩一个值或者区间不存在直接返回
	if (begin >= end)
	{
		return;
	}

	int left = begin, right = end;
	int key = v[begin];
	int piti = begin;
	while (left < right)
	{
		//右边先走，找到比key小的就停下来
		while (left < right && v[right] >= key)
		{
			right--;
		}

		v[piti] = v[right];
		piti = right;

		//左边走，找到比key大的就停下来
		while (left < right && v[left] <= key)
		{
			left++;
		}

		v[piti] = v[left];
		piti = left;
	}
	
	v[piti] = key;

	//左区间
	QuickSort(v, begin, piti - 1);
	//右区间
	QuickSort(v, piti + 1, end);
}

 前后指针法

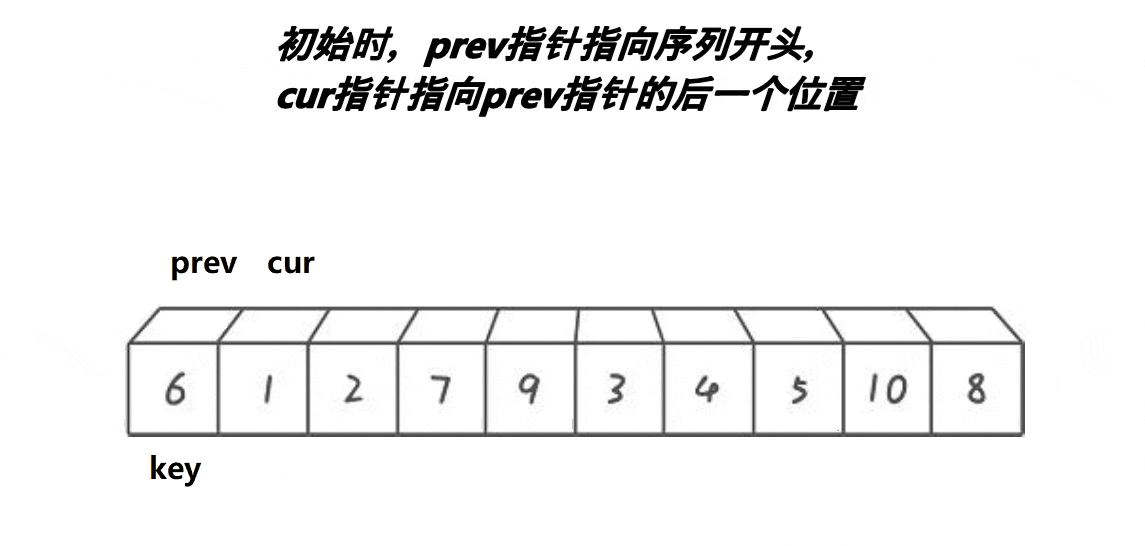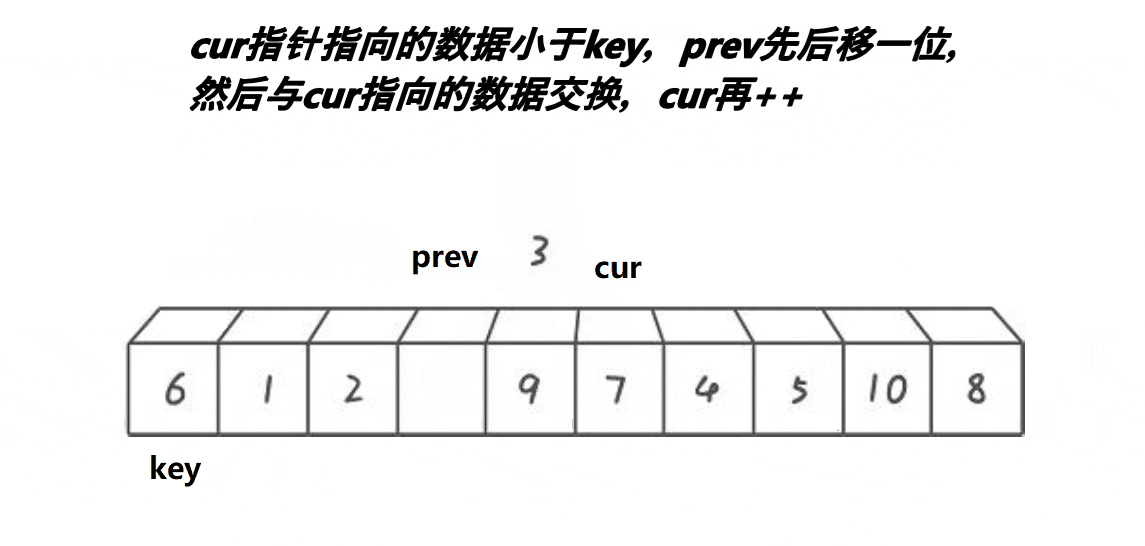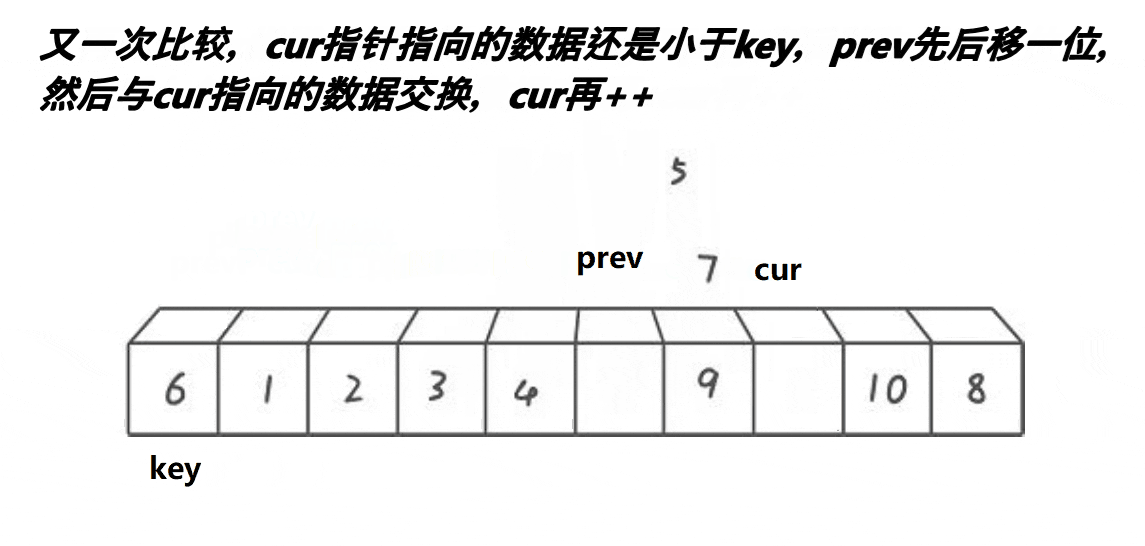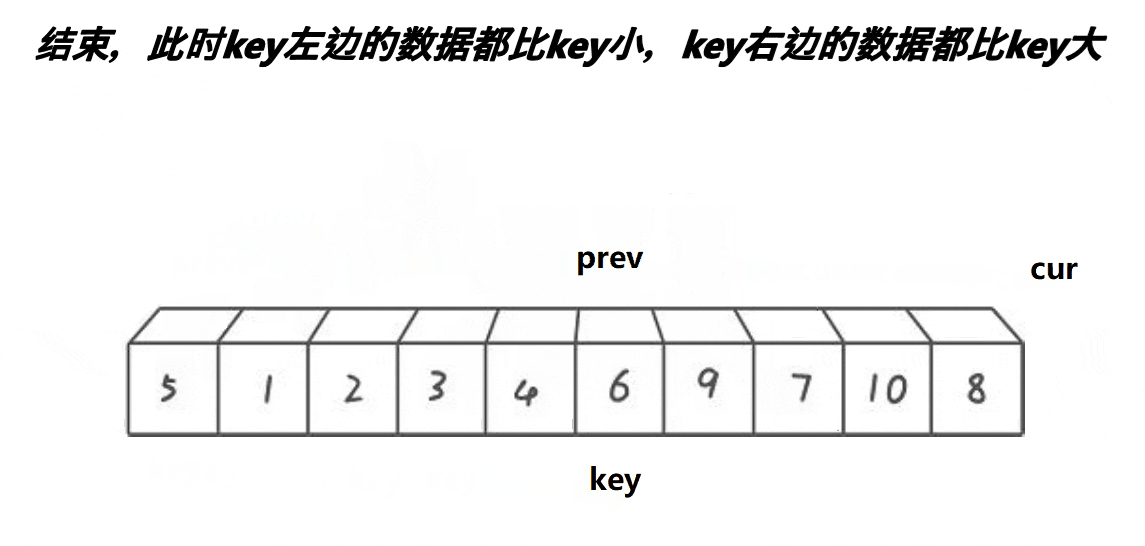
代码实现： 

void QuickSort(vector<int>& v, int begin, int end)
{
	//如果只剩一个值或者区间不存在直接返回
	if (begin >= end)
	{
		return;
	}

	int prev = begin, cur = prev + 1;
	int keyi = begin;

	while (cur <= end)
	{
		if (v[cur] < v[keyi] && ++prev != cur)
			Swap(v[prev], v[cur]);

		cur++;
	}
	Swap(v[prev], v[keyi]);
	keyi = prev;

	//左区间
	QuickSort(v, begin, keyi - 1);
	//右区间
	QuickSort(v, keyi + 1, end);
}

 非递归版本

递归的问题，在极端场景下如果深度太深，会出现栈溢出，所以我们要改成非递归版本

我这里就用个栈来模拟递归过程，当然你用个队列来实现也是可以的。

int PartQuickSort(vector<int> &v, int begin, int end)
{
	int key = v[begin];
	int piti = begin;
	while (begin < end)
	{
		//右边先走，找到比key小的就停下来
		while (begin < end && v[end] >= key)
		{
			end--;
		}

		v[piti] = v[end];
		piti = end;

		//左边走，找到比key大的就停下来
		while (begin < end && v[begin] <= key)
		{
			begin++;
		}

		v[piti] = v[begin];
		piti = begin;
	}
	v[piti] = key;
	return piti;

}

//利用栈来模拟递归从场景—栈是先进后出
void QuickSortNonR(vector<int> &v, int begin, int end)
{
	stack<int> st;
	//先入右在入左
	st.push(end);
	st.push(begin);

	while (!st.empty())
	{
		int left = st.top();
		st.pop();

		int right = st.top();
		st.pop();

		int keyi = PartQuickSort(v, left, right);

		//左区间入栈
		if (left < keyi - 1)
		{
			st.push(keyi - 1);
			st.push(left);
		}
		
		//右区间入栈
		if (keyi + 1 < right)
		{
			st.push(right);
			st.push(keyi + 1);
		}
	}
}

快速排序中的优化

//三个数取中间值做为key
int GetMidKeyi(vector<int>& v, int begin, int end)
{
	int mid = (begin + end) / 2;
	if (v[begin] < v[mid])
	{
		if (v[mid] < v[end])
		{
			return mid;
		}
		else if (v[begin] < v[end])
		{
			return end;
		}
		else
		{
			return begin;
		}
	}
	else//v[begin] > v[mid]
	{
		if (v[mid] > v[end])
		{
			return mid;
		}
		else if (v[begin] < v[end])
		{
			return begin;
		}
		else
		{
			return end;
		}
	}
}

归并排序

动图演示

代码实现：

递归版本

//归并排序—时间复杂度O(N*logN)
//空间复杂度O(N)
void _MergeSort(vector<int> &v, int begin, int end, vector<int> &tmp)
{
	//递归返回的条件
	if (begin >= end)
		return;

	int mid = (begin + end) / 2;

	//进行递归
	_MergeSort(v, begin, mid, tmp);
	_MergeSort(v, mid + 1, end, tmp);

	int begin1 = begin, end1 = mid;
	int begin2 = mid + 1, end2 = end;
	int i = begin1;
	while (begin1 <= end1 && begin2 <= end2)
	{
		if (v[begin1] < v[begin2])
		{
			tmp[i++] = v[begin1++];
		}
		else
		{
			tmp[i++] = v[begin2++];
		}
	}

	//如果后面还有数，也要拷贝到tmp中去
	while (begin1 <= end1)
		tmp[i++] = v[begin1++];

	while (begin2 <= end2)
		tmp[i++] = v[begin2++];

	//深拷贝
	int j = begin, k = end - begin + 1;
	while(k-- && j <= end)
	{
		v[j] = tmp[j];
		j++;
	}
}


void MergeSort(vector<int> &v, int n)
{
	vector<int> tmp(n, 0);
	_MergeSort(v, 0, n - 1, tmp);
}

非递归版本

//非递归版本
void MergeSortNonR(vector<int>& v, int n)
{
	vector<int> tmp(n, 0);

	int gap = 1;
	while (gap < n)
	{
		for (int i = 0; i < n; i += 2 * gap)
		{
			int begin1 = i, end1 = i + gap - 1;
			int begin2 = i + gap, end2 = i + 2 * gap - 1;

			//修正边界,防止越界
			if (end1 >= n)
			{
				end1 = n - 1;
				begin2 = n;
				end2 = n - 1;
			}
			else if (begin2 >= n)
			{
				begin2 = n;
				end2 = n - 1;
			}
			else if (end2 >= n)
			{
				end2 = n - 1;
			}


			int j = begin1;
			while (begin1 <= end1 && begin2 <= end2)
			{
				if (v[begin1] < v[begin2])
				{
					tmp[j++] = v[begin1++];
				}
				else
				{
					tmp[j++] = v[begin2++];
				}
			}

			//如果后面还有数，也要拷贝到tmp中去
			while (begin1 <= end1)
				tmp[j++] = v[begin1++];

			while (begin2 <= end2)
				tmp[j++] = v[begin2++];
		}

		//深拷贝
		for (int k = 0; k < n; k++)
		{
			v[k] = tmp[k];
		}

		gap *= 2;
	}
}

或者

void MergeSortNonR(vector<int>& v, int n)
{
	vector<int> tmp(n, 0);

	int gap = 1;
	while (gap < n)
	{
		for (int i = 0; i < n; i += 2 * gap)
		{
			int begin1 = i, end1 = i + gap - 1;
			int begin2 = i + gap, end2 = i + 2 * gap - 1;

			//修正边界,防止越界
			if (end1 >= n || begin2 >= n)
			{
				break;
			}
			else if (end2 >= n)
			{
				end2 = n - 1;
			}

			int k = end2 - begin1 + 1;
			int j = begin1;
			while (begin1 <= end1 && begin2 <= end2)
			{
				if (v[begin1] < v[begin2])
				{
					tmp[j++] = v[begin1++];
				}
				else
				{
					tmp[j++] = v[begin2++];
				}
			}

			//如果后面还有数，也要拷贝到tmp中去
			while (begin1 <= end1)
				tmp[j++] = v[begin1++];

			while (begin2 <= end2)
				tmp[j++] = v[begin2++];

			int m = i;
			while (k-- && m < n)
			{
				v[m] = tmp[m];
				m++;
			}
		}

		gap *= 2;
	}
}

计数排序

代码实现：

//计数排序
//时间复杂度：O(max(range,N))
//空间复杂度：O(range)
void CountSort(vector<int>& v, int n)
{
	int max = v[0], min = v[0];
	for (auto vv : v)
	{
		if (vv < min)
			min = vv;

		if (vv > max)
			max = vv;
	}

	int range = max - min + 1;
	vector<int> count(range, 0);

	//统计次数
	for (int i = 0; i < n; i++)
	{
		count[v[i] - min]++;
	}

	//回写排序
	int j = 0;
	for (int i = 0; i < range; i++)
	{
		while (count[i]--)
		{
			v[j++] = i + min;
		}
	}
}

 总结

计数排序在这里不做比较。 

今天的分享就到这里，如果觉得有所收获的话，就给博主三连吧，创作不易，你的支持将是我创作的动力。

谢谢！！！