1.1逻辑代数
1.逻辑代数概述
乔治.布尔是逻辑代数的奠基人,所以又称布尔代数。
1.2布尔代数常用公式
1.几个基础公式
- 常量与常量之间:与,或,非。
- 常量与变量之间:
a. 0-1律:A+1=1 A*0=0
b.自等率:A*1=A A+0=A
c.重叠率:A*A=A A+A=A
d.互补律:A*A非=0 A+A非=1
e.交换律,结合律,分配律

2.化简公式
- 吸收定律

- 多余项定理
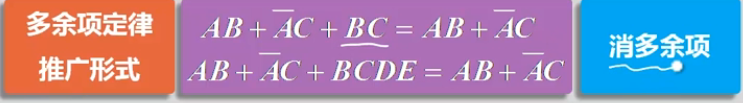
3.求反公式(摩根定律)
与之非等于非之或 ,或之非等于非之与。

摩根定律推广之运算复杂时,与和或对调,原变量与反变量对调,0和1对调,但是长非号不变,运算优先级不变。(反演定律)
4.逻辑运算优先级
括号,长非号>与(逻辑×)>异或,同或>或(逻辑加)
1.3 基本定律
1.带入定律:在任何包含变量A的逻辑公式中,若以另外一个逻辑表达式带入公式A的位置,公式仍然成立。
2.反演定律:同上所示;
3.对偶定律:与或对调,0和1对调,变量不变,长非号不变,保证原先优先级不变。其中异或和同或均互为对偶式。
1.4逻辑函数的5类基本形式
第一种:最简与或式;
第二种:与非——与非式(与或式两次取反,用摩根定律展开一层)
第三种:与或非式(原始求其反函数的与或式,再取一次反)
第四种:或与式(与或非式用摩根定律展开两层,得到或与式)
第五种:或非——或非(或与式两次取反,在用摩根定律展开一层)









