目录
算法的定义,从数学角度,算法是用于解决某一类问题的公式和思想。计算机角度,算法是一系列程序指令,用于解决特定的运算和逻辑问题。其研究的目的是为了更有效的处理数据,提高数据运算效率。
如何衡量算法的好坏:时间复杂度:运行时间长短。空间复杂度:占用内存大小。
怎么计算时间复杂度:大O表示法(渐进时间复杂度):把程序的相对执行时间函数T(n)简化为一个数量级,这个数量级可以是n、n^2、logN等。推导时间复杂度的几个原则:如果运行时间是常数量级,则用常数1表示。只保留时间函数中的最高阶项。如果最高阶项存在,则省去最高项前面的系数。时间复杂度对比:O(1) > O(logn) > O(n) > O(nlogn) > O(n^2)。不同时间复杂度算法运行次数对比
怎么计算空间复杂度
常量空间 O(1):存储空间大小固定,和输入规模没有直接的关系。线性空间 O(n):分配的空间是一个线性的集合,并且集合大小和输入规模n成正比。二维空间 O(n^2):分配的空间是一个二维数组集合,并且集合的长度和宽度都与输入规模n成正比。递归空间 O(logn):递归是一个比较特殊的场景。虽然递归代码中并没有显式的声明变量或集合,但是计算机在执行程序时,会专门分配一块内存空间,用来存储“方法调用栈”。执行递归操作所需要的内存空间和递归的深度成正比。
如何定义算法的稳定性
稳定:如果a原本在b前面,而a=b,排序之后a仍然在b的前面。不稳定:如果a原本在b的前面,而a=b,排序之后 a 可能会出现在 b 的后面。
有哪些常见算法
- 字符串:暴力匹配、BM、KMP、Trie等。
- 查找:二分查找、遍历查找等。
- 排序:冒泡排序、快排、计数排序、堆排序等。
- 搜索:TFIDF、PageRank等。
- 聚类分析:期望最大化、k-meanings、k-数位等。
- 深度学习:深度信念网络、深度卷积神经网络、生成式对抗等。
- 异常检测:k最近邻、局部异常因子等。
- ......
十大经典排序算法

性能对比 随机生成区间0 ~ K之间的序列,共计N个数字,利用各种算法进行排序,记录排序所需时间。

字符串算法
字符串匹配算法
BF算法,是Brute Force(暴力算法)的缩写,是一种字符串匹配算法。
算法步骤
问题:两个字符串a和b,判断b是否是a的子串,如果是请返回b在a中第一次出现的位置。
1.第一轮,从字符串a的首位开始,把a和b的字符逐个比较,a的首位字符是a,b的首位字符是b,不匹配。
2.第二轮,把字符串b后移动一位,从a字符串第二位开始逐个对比。a串的第二位和b串的第二位都是b,继续比较,a串的第三位(b)与b串的第三位(c)不匹配。
3.第三轮,再把b串往后移动一位,从a串的第三位开始,与b串依次逐个比较。a串的第三位字符是b,b串的第三位字符也是b,第四位字符是c,b串的第四位字符也是c,第五位都是e,两者匹配
比较完成。由此得出的结论是b串是a串的子串,在主串中第一次出现的位置下标是2。
示例代码
public static void main(String[] args) throws Exception {
String a = "abbcefgh";
String b = "bce";
int num = bruteForceSearchPatternInText(a, b);
}
public static int bruteForceSearchPatternInText(String text, String pattern) {
int sLen = text.length();
int pLen = pattern.length();
char[] s = text.toCharArray();
char[] p = pattern.toCharArray();
while (sLen < pLen) {
return -1;
}
int i = 0;
int j = 0;
while (i < sLen && j < pLen) {
if (s[i] == p[j]) {
//如果当前字符匹配成功(即S[i] == P[j]),则i++,j++
i = i + 1;
j = j + 1;
} else {
//如果失配(即S[i]! = P[j]),令i = i - (j - 1),j = 0
i = i - (j - 1);
j = 0;
}
}
//匹配成功,返回模式串p在文本串s中的位置,否则返回-1
if (j == pLen) {
return i - j;
} else {
return -1;
}
}RK算法
如果 a = "aaaaaaaaaaaaaaaaab" b="aaab";像这种情况每一轮的检查都需要匹配到b串的最后一个字符,才发现不匹配,两个字符串在每一轮都要比较四次,假设a串长度为m,b串长度为n那么在这种极端的情况下,BF算法的最坏时间复杂度是O(mn),如何让时间复杂度变为O(n) 有什么更优的解决方案呢?用RK算法呀
RK算法全称Rabin-Karp是由算法的两位发明者Rabin和Karp的名字来命名的。BF算法只是对两个字符串的所有字符依次比较,而RK算法比较的是两个字符串的哈希值。
RK算法步骤
1.生成b串的hashcode
2.生成a串中第一个等长子串的hashcode(abb的hashcode)
3.比较两个hashcode
4.a串中第二个等长子串的hashcode(bbc的hashcode)
5.比较两个hashcode
6.生成a串当中第三个等长子串的hashcode(bce的hashcode)
7.比较两个hashcode
8.依次对比,直到找到两个相同的hashcode,然后像BF算法那样,对两个相同hashcode的字符串逐个字符比较,最终判断两个字符串匹配。
代码
public static void main(String[] args) throws Exception {
String str = "aacdesadsdfer";
String pattern = "adsd";
System.out.println("第一次出现的位置:" + rabinKarp(str, pattern));
}
public static int rabinKarp(String str, String pattern) {
//主串长度
int m = str.length();
//b串的长度
int n = pattern.length();
//计算b串的hash值
int patternCode = hash(pattern);
//计算主串当中第一个和b串等长的子串hash值
int strCode = hash(str.substring(0, n));
//用b串的hash值和主串的局部hash值比较。
//如果匹配,则进行精确比较;如果不匹配,计算主串中相邻子串的hash值。
for (int i = 0; i < m - n + 1; i++) {
if (strCode == patternCode && compareString(i, str, pattern)) {
return i;
}
//如果不是最后一轮,更新主串从i到i+n的hash值
if (i < m - n) {
strCode = nextHash(str, strCode, i, n);
}
}
return -1;
}
private static int hash(String str) {
int hashcode = 0;
//这里采用最简单的hashcode计算方式:
//把a当做1,把b当中2,把c当中3.....然后按位相加
for (int i = 0; i < str.length(); i++) {
hashcode += str.charAt(i) - 'a';
}
return hashcode;
}
private static int nextHash(String str, int hash, int index, int n) {
hash -= str.charAt(index) - 'a';
hash += str.charAt(index + n) - 'a';
return hash;
}
private static boolean compareString(int i, String str, String pattern) {
String strSub = str.substring(i, i + pattern.length());
return strSub.equals(pattern);
}
RK算法缺点
RK算法计算单个子串hash的时间复杂度是O(n),但是由于后续的子串hash是增量计算,所以总的时间复杂度是O(n)。那么RK算法有什么不足之处呢,RK算法的缺点在于哈希冲突,每次hash冲突的时候,RK算法都要对 子串和b串进行逐个字符的比较,如果冲突太多,RK算法就退化成了BF算法。
KMP
KMP全称为Knuth Morris Pratt算法,三个单词分别是三个作者的名字。KMP是一种高效的字符串匹配算法,用来在主字符串中查找模式字符串的位置(比如在"hello,world"主串中查找"world"模式串的位置)。
KMP算法的高效体现在哪
高效性是通过和其他字符串搜索算法对比得到的,在这里拿BF(Brute Force)算法做一下对比。BF算法是一种最朴素的暴力搜索算法。它的思想是在主串的[0, n-m]区间内依次截取长度为m的子串,看子串是否和模式串一样(n是主串的长度,m是子串的长度)。BF的时间复杂度是O(N乘以N),存在很大优化空间。当模式串和主串匹配时,遇到模式串中某个字符不能匹配的情况,对于模式串中已经匹配过的那些字符,如果我们能找到一些规律,将模式串多往后移动几位,而不是像BF算法一样,每次把模式串移动一位,就可以提高算法的效率。比如说在"ababaababacd"中查找"ababac",可以避免一些字符之间的比较。
KMP算法的next数组
明确next数组的含义 : next数组用来存模式串中每个前缀最长的能匹配前缀子串的结尾字符的下标。 next[i] = j 表示下标以i-j为起点,i为终点的后缀和下标以0为起点,j为终点的前缀相等,且此字符串的长度最长。用符号表示为p[0j] == p[i-ji]。下面以"ababacd"模式串为例,给出这个串的next数组。
算法流程
举例来说,有一个字符串"BBC ABCDAB ABCDABCDABDE",我想知道,里面是否包含另一个字符串"ABCDABD"?
- 字符串"BBC ABCDAB ABCDABCDABDE"的第一个字符与搜索词"ABCDABD"的第一个字符,进行比较。B与A不匹配,搜索词后移一位。
- 然后第二个字符B与A不匹配,搜索词再往后移。直到字符串有一个字符,与搜索词的第一个字符相同为止。
- 然后比较字符串和搜索词的下一个字符,还是相同。直到字符串有一个字符,与搜索词对应的字符不相同为止,这时,最自然的反应是,将搜索词整个后移一位,再从头逐个比较。这样做虽然可行,但是效率很差,因为你要把"搜索位置"移到已经比较过的位置,重比一遍。
- 已知空格与D不匹配时,前面六个字符"ABCDAB"是匹配的。查表可知,最后一个匹配字符B对应的"部分匹配值"为2,因此按照下面的公式算出向后移动的位数:移动位数 = 已匹配的字符数 - 对应的部分匹配值,因为 6 - 2 等于4,所以将搜索词向后移动4位。
- 然后发现空格与C不匹配,搜索词还要继续往后移。这时,已匹配的字符数为2("AB"),对应的"部分匹配值"为0。所以,移动位数 = 2 - 0,结果为 2,于是将搜索词向后移2位。
- 然后空格与A不匹配,继续后移一位。
- 逐位比较,直到发现C与D不匹配。于是,移动位数 = 6 - 2,继续将搜索词向后移动4位。
- 逐位比较,直到搜索词的最后一位,发现完全匹配,于是搜索完成。如果还要继续搜索(即找出全部匹配),移动位数 = 7 - 0,再将搜索词向后移动7位,这里就不再重复了。
KMP的时间复杂度
KMP的时间复杂度是O(n)。
示例
/**
* KMP算法
*
* @param ss 主串
* @param ps 模式串
* @return 如果找到,返回在主串中第一个字符出现的下标,否则为-1
*/
public static int KMP(String ss, String ps) {
char[] s = ss.toCharArray();
char[] p = ps.toCharArray();
int i = 0; // 主串的位置
int j = 0; // 模式串的位置
int[] next = getNext(ps);
while (i < s.length && j < p.length) {
//①如果j=-1,或者当前字符匹配成功(即S[i]==P[j]),都令i++,j++
if (j == -1 || s[i] == p[j]) { // 当j为-1时,要移动的是i,当然j也要归0
i++;
j++;
} else {
//②如果j!=-1,且当前字符匹配失败(即S[i]!=P[j]),则令i不变,j=next[j],j右移j-next[j]
j = next[j];
}
}
if (j == p.length) {
return i - j;
} else {
return -1;
}
}BM匹配算法
BM算法也是一种精确字符串匹配算法,它采用从右向左比较的方法,同时应用到了两种启发式规则,即坏字符规则 和好后缀规则 ,来决定向右跳跃的距离。基本思路就是从右往左进行字符匹配,遇到不匹配的字符后从坏字符表和好后缀表找一个最大的右移值,将模式串右移继续匹配。
替换空格
请实现一个函数,将一个字符串中的每个空格替换成“%20”。例如,当字符串为We Are Happy.则经过替换之后的字符串为We%20Are%20Happy。
public class Solution {
public String replaceSpace(StringBuffer str) {
StringBuffer res = new StringBuffer();
int len = str.length() - 1;
for(int i = len; i >= 0; i--){
if(str.charAt(i) == ' ')
res.append("02%");
else
res.append(str.charAt(i));
}
return res.reverse().toString();
}
}
最长公共前缀
编写一个函数来查找字符串数组中的最长公共前缀。如果不存在公共前缀,返回空字符串 "" 例如:输入["flowers"," flow","flight"] 输出:"fl"
public class Solution {
public String longestCommonPrefix(String[] strs) {
if(strs == null || strs.length == 0)
return "";
Arrays.sort(strs);
char [] first = strs[0].toCharArray();
char [] last = strs[strs.length - 1].toCharArray();
StringBuffer res = new StringBuffer();
int len = first.length < last.length ? first.length : last.length;
int i = 0;
while(i < len){
if(first[i] == last[i]){
res.append(first[i]);
i++;
}
else
break;
}
return res.toString();
}
}查找类算法
递归查找
public static int Add(int i) {
if (i <= 100) {
count += i;
Add(i + 1);
}
return count;
}顺序查找
说明
顺序查找适合于存储结构为顺序存储或链接存储的线性表。
基本思想
顺序查找也称为线形查找,属于无序查找算法。从数据结构线形表的一端开始,顺序扫描,依次将扫描到的结点关键字与给定值k相比较,若相等则表示查找成功,若扫描结束仍没有找到关键字等于k的结点,表示查找失败。
复杂度分析
查找成功时的平均查找长度为:(假设每个数据元素的概率相等) ASL = 1/n(1+2+3+…+n) = (n+1)/2;当查找不成功时,需要n+1次比较,时间复杂度为O(n),所以顺序查找的时间复杂度为O(n)。
示例
public class sequence{
public static boolean SequenceSearch(int a[],int k,int value){
for(int i=0;i<k;i++){
if(value == a[i]){
return true;
}else{
return false;
}
}
public static void main(String[] args) {
int[] a = {8,2,4,5,3,10,11,6,9};
System.out.println(SequenceSearch(a,a.length,20));
}
}二分查找法
说明
元素必须是有序的,如果是无序的要先进行排序操作。也称为是折半查找,属于有序查找算法。
基本思想
用给定值k先与中间结点的关键字比较,中间结点把线形表分成两个子表,若相等则查找成功,若不相等,再根据k与该中间结点关键字的比较结果确定下一步查找哪个子表,这样递归进行,直到查找到或查找结束发现表中没有这样的结点。
复杂度分析
最坏情况下,关键词比较次数为log2(n+1),且期望时间复杂度为O(log2n)。折半查找的前提条件是需要有序表顺序存储,对于静态查找表,一次排序后不再变化,折半查找能得到不错的效率。但对于需要频繁执行插入或删除操作的数据集来说,维护有序的排序会带来不小的工作量,那就不建议使用。
特点
比较次数少,查找速度快 但是排序的数组必须是有序的。
示例
public static int binarySearch(int a[], int key) {
int left = 0;
int right = a.length - 1;
int mid;
while (left <= right) {
mid = (left + right) / 2;
if (key == a[mid]){
return mid;
}
if (key < a[mid]){
right = mid - 1; //right = mid时,能会死循环
}else{
left = mid + 1; //left = mid时,可能死循环
}
}
return -1;
}查找算法
根据给定的某个值,在查找表中确定一个其关键字等于给定值的数据元素(或记录)。查找是在大量的信息中寻找一个特定的信息元素,在计算机应用中,查找是常用的基本运算。
查找算法分类:
1.静态查找和动态查找。
静态或者动态都是针对查找表而言的。动态表指查找表中有删除和插入操作的表。
2.无序查找和有序查找。
无序查找:被查找数列有序无序均可。
有序查找:被查找数列必须为有序数列。
平均查找长度(Average Search Length,ASL):需和指定key进行比较的关键字的个数的期望值,称为查找算法在查找成功时的平均查找长度。对于含有n个数据元素的查找表,查找成功的平均查找长度为:ASL = Pi*Ci的和。Pi:查找表中第i个数据元素的概率。Ci:找到第i个数据元素时已经比较过的次数。
Hash算法
任意长度的输入经过Hash算法转化为一定长度的输出。
举个例子:读很多本书,最终总结成一本摘要,
看书的操作可以理解为hash算法,总结一本摘要可以理解为hash值。 所以hash算法也称为摘要算法或者散列算法。
特点
- 不可逆:不能通过hash值计算出原本的值。
- 效率高:hash算法通常能够快速的得到结果。
- 冲突少:优秀的hash算法应具备的条件。
Hash应用
-
密码学及数字签名
我们登陆知乎的时候都需要输入密码,那么知乎如果明文保存这个密码,那么黑客就很容易窃取大家的密码来登陆, 特别不安全。那么知乎就想到了一个方法,使用hash算法生成一个密码的签名,知乎后台只保存这个签名值。 由于hash算法是不可逆的,那么黑客即便得到这个签名,也丝毫没有用处;而如果你在网站登陆界面上输入你的密码, 那么知乎后台就会重新计算一下这个hash值,与网站中储存的原hash值进行比对,如果相同, 证明你拥有这个账户的密码,那么就会允许你登陆。 -
文件完整性校验
目前流行的 Hash 算法包括 MD5、SHA-1 和 SHA-2。 MD4(RFC 1320)是 MIT 的 Ronald L. Rivest 在 1990 年设计的,MD 是 Message Digest 的缩写。 其输出为 128 位。MD4 已证明不够安全。MD5(RFC 1321)是 Rivest 于1991年对 MD4 的改进版本。 它对输入仍以512位分组,其输出是 128 位。MD5比MD4复杂,并且计算速度要慢一点,更安全一些。 MD5 已被证明不具备”强抗碰撞性”。SHA (Secure Hash Algorithm)是一个 Hash 函数族, 由 NIST(National Institute of Standards and Technology)于1993年发布第一个算法。 目前知名的 SHA-1 在1995年面世,它的输出为长度 160 位的hash值,因此抗穷举性更好。 SHA-1 设计时基于和 MD4 相同原理,并且模仿了该算法。SHA-1已被证明不具”强抗碰撞性”。 为了提高安全性,NIST 还设计出了 SHA-224、SHA-256、SHA-384,和 SHA-512 算法(统称为 SHA-2), 跟 SHA-1 算法原理类似。SHA-3 相关算法也已被提出 例子: import hashlib # 两段HEX字节串,注意它们有细微差别 a = bytearray.fromhex("0e306561559aa787d00bc6f70bbdfe3404cf03659e704f8534c00ffb659c4 c8740cc942feb2da115a3f4155cbb8607497386656d7d1f34a42059d78f5a8dd1ef") b = bytearray.fromhex("0e306561559aa787d00bc6f70bbdfe3404cf03659e744f8534c00ffb659c4 c8740cc942feb2da115a3f415dcbb8607497386656d7d1f34a42059d78f5a8dd1ef") # 输出MD5,它们的结果一致 print(hashlib.md5(a).hexdigest()) print(hashlib.md5(b).hexdigest()) ### a和b输出结果都为: cee9a457e790cf20d4bdaa6d69f01e41 cee9a457e790cf20d4bdaa6d69f01e41 文件内容a和b有细微的修改,得到的hash值应该不一样才对,所以MD5在数年前就已经不被推荐作为应用中的 散列算法方案,取代它的是SHA家族算法,也就是安全散列算法(Secure Hash Algorithm,缩写为SHA) -
高级语言比如JAVA中基于Hash的数据结构
HashMap是对Array与Link的折衷处理,Array与Link可以说是两个速度方向的极端,Array注重于数据的获取, 而处理修改(添加/删除)的效率非常低;Link由于是每个对象都保持着下一个对象的指针,查找某个数据需要 遍历之前所有的数据,所以效率比较低,而在修改操作中比较快。 JDK1.8,HashMap中Hash值的计算: static final int hash(Object key) { int h; //计算hashCode return (key == null) ? 0 : (h = key.hashCode()) ^ (h >>> 16); } Java中几个常用的哈希码(hashCode)的算法。 1.Object类的hashCode. 返回对象的经过处理后的内存地址,由于每个对象的内存地址都不一样,所以哈希码也不一样。 这个是native方法,取决于JVM的内部设计,一般是某种C地址的偏移。 2.String类的hashCode. 根据String类包含的字符串的内容,根据一种特殊算法返回哈希码,只要字符串的内容相同, 返回的哈希码也相同。 3.Integer等包装类,返回的哈希码就是Integer对象里所包含的那个整数的数值, 例如Integer i1=new Integer(100), i1.hashCode的值就是100 。 由此可见,2个一样大小的Integer对象,返回的哈希码也一样 JDK中的String.hashCode(): public int hashCode() { int h = hash; //hash default value : 0 if (h == 0 && value.length > 0) { //value : char storage char val[] = value; for (int i = 0; i < value.length; i++) { h = 31 * h + val[i]; } hash = h; } return h; }
Hash冲突
当Key值利用Hash算法定位到数组的某个位置,该位置已经有值时,产生冲突:利用链表解决,称为链地址法;向下线性或者随机探测不冲突的地址称为开放地址法,也可以通过多个hash算法重新定位称为再Hash法
排序类算法
冒泡排序
- 1、比较相邻的两个元素如果第一个比第二个大,就交换它们的位置。
- 2、然后第二个与第三个对比,对每一对相邻元素作同样的工作,这样在最后的元素应该会是最大的数。
- 3、针对所有的元素重复以上的步骤,除了最后一个。
- 4、重复步骤1~3,直到排序完成。

示例
int a[] = {6, 3, 4, 2, 10, 1 ,8,5,9};
for (int i = 0; i<a.length-1; i++) {
for (int j = 0; j<a.length-1-i; j++) {
if (a[j] > a[j + 1]) {
int temp = a[j];
a[j] = a[j + 1];
a[j + 1] = temp;
}
}
}
优缺点
优点:实现和理解简单。缺点:时间复杂度是O(n^2),排序元素多时效率比较低。
适用范围
数据已经基本有序,且数据量较小的场景。
场景优化
-
(1)部分已经有序了,下一轮的时候但还是会被遍历:记录有序和无序数据的边界,有序的部分在下一轮就不用遍历了。
-
(2)在每趟扫描中,记住最后一次交换发生的位置lastExchange,(该位置之后的相邻记录均已有序)。下一趟排序开始时,R[1..lastExchange-1]是无序区,R[lastExchange..n]是有序区。这样,一趟排序可能使当前无序区扩充多个记录,因此记住最后一次交换发生的位置lastExchange,从而减少排序的趟数
在每趟排序开始前,先将其置为0。若排序过程中发生了交换,则将其置为1。各趟排序结束时检查flag,若未曾发生过交换则终止算法,不再进行下一趟排序。 int flag = 0; for (int i = 0; i<a.length-1; i++) { for (int j = 0; j<a.length-1-i; j++) { if (a[j] > a[j + 1]) { int temp = a[j]; a[j] = a[j + 1]; a[j + 1] = temp; flag = 1;//只要有发生了交换,flag就置为1 } } //判断标志位是否为0,如果为0,说明后面的元素已经有序,就直接return if (flag == 0){ return; } }
选择排序(Selection-sort)
选择排序(Selection sort)也是一种简单直观的排序算法。
算法描述
1)首先在未排序序列中找到最小(大)元素,存放到排序序列的起始位置
2)再从剩余未排序元素中继续寻找最小(大)元素,然后放到已排序序列的末尾。
3)重复第二步,直到所有元素均排序完毕。
示例
for (int i = 0; i < a.length - 1; i++) {
for (int j = i + 1; j < a.length; j++) {
if (a[i] > a[j]) {
int temp = a[i];
a[i] = a[j];
a[j] = temp;
}
}
}
插入法排序
插入排序(Insertion-Sort)是一种简单直观且稳定的排序算法。如果有一个已经有序的数据序列,要求在这个已经排好的数据序列中插入一个数,但要求插入后此数据序列仍然有序,这个时候就要用到插入排序了。
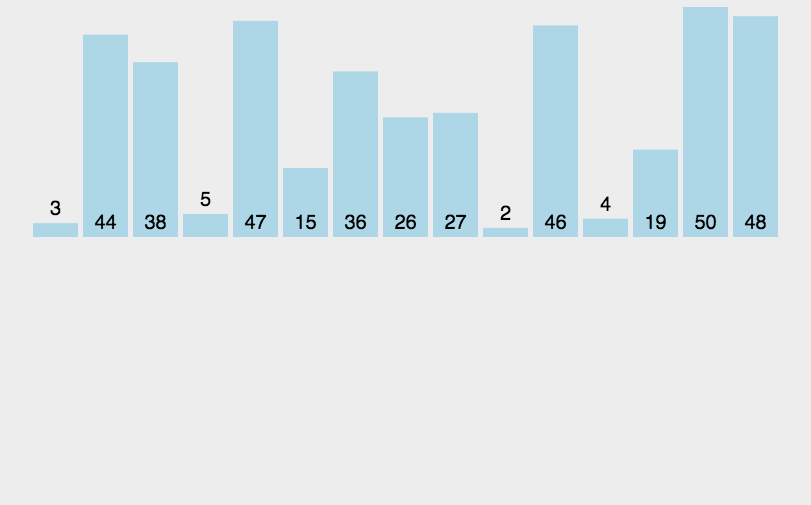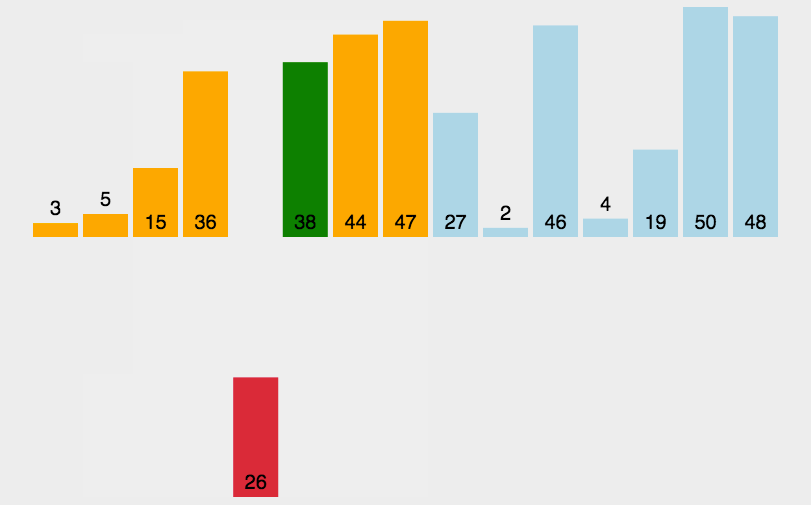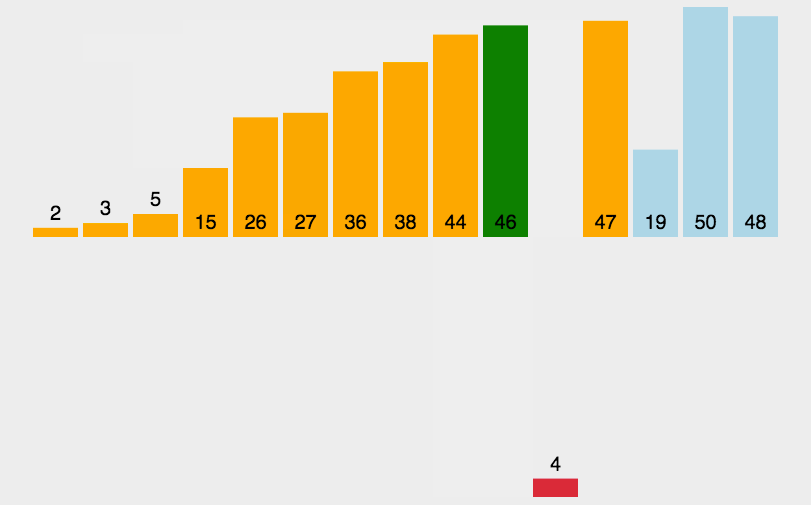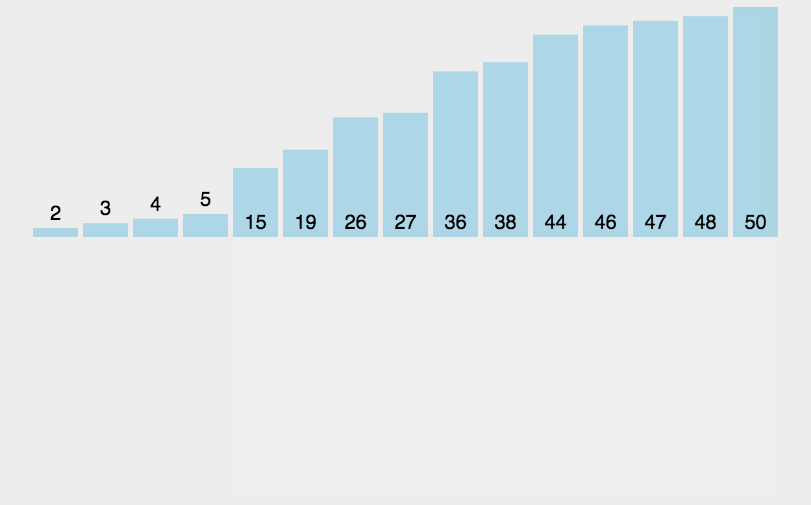
基本思想
它的工作原理是通过构建有序序列,对于未排序数据,在已排序序列中从后向前扫描,找到相应位置并插入。
操作步骤
将第一待排序序列第一个元素看做一个有序序列,把第二个元素到最后一个元素当成是未排序序列。从头到尾依次扫描未排序序列,将扫描到的每个元素插入有序序列的适当位置。(如果待插入的元素与有序序列中的某个元素相等,则将待插入元素插入到相等元素的后面,这样做让插入排序变得稳定)通俗地讲,如果我们有五张扑克牌{8,4,6,5,9},我们想要把它整理成从小到大的序列,那么我们先把8作为“基准”,也就是我们把序列{8}作为有序序列,然后4应该插入到序列{8}的前面,这样有序序列就变为{4,8},接下来我们把6插入到{4,8}中,只需要从后往前遍历有序序列,直到有序序列中的元素小于或等于要插入的元素,这样我们得到有序序列{4,6,8},再把5插入其中,得到有序序列{4,5,6,8},最后得到有序序列{4,5,6,8,9},这样我们的插入排序就完成了。
示例
代码1:
// 插入排序
for (int i = 0; i < a.length - 1; i++) {
for (int j = i + 1; j > 0; j--) {
if (a[j] < a[j - 1]) {
int temp = a[j];
a[j] = a[j - 1];
a[j - 1] = temp;
}
}
}
for (int b : a) {
System.out.print("" + b);
}
代码2:
int i,j;
long startTime = System.nanoTime(); // 获取排序开始时间
for( i=1;i<a.length;i++) {
int temp=a[i];
for( j = i-1;j>=0&&temp<a[j];j--) {
a[j+1]=a[j];
}
a[j+1]=temp;
}
long endTime = System.nanoTime(); // 获取排序结束时间
System.out.println("排序結果:" + Arrays.toString(a));
System.out.println("程序运行时间: " + (endTime - startTime) + "ns");
三数取中+插入排序
插入排序在元素个数较少时效率是最高的,可以设定一个阈值,当元素个数大于阈值时使用快速排序,小于等于该阈值时则使用插入排序。我们设定阈值为 7 。
private static final int INSERTION_SORT_MAX_LENGTH = 7;
public int[] sortArray(int[] nums) {
quickSort(nums,0,nums.length-1);
return nums;
}
public void quickSort (int[] nums, int low, int hight) {
if (hight - low <= INSERTION_SORT_MAX_LENGTH) {
insertSort(nums,low,hight);
return;
}
int index = partition(nums,low,hight);
quickSort(nums,low,index-1);
quickSort(nums,index+1,hight);
}
public int partition (int[] nums, int low, int hight) {
//三数取中,大家也可以使用其他方法
int mid = low + ((hight-low) >> 1);
if (nums[low] > nums[hight]) swap(nums,low,hight);
if (nums[mid] > nums[hight]) swap(nums,mid,hight);
if (nums[mid] > nums[low]) swap(nums,mid,low);
int pivot = nums[low];
int start = low;
while (low < hight) {
while (low < hight && nums[hight] >= pivot) hight--;
while (low < hight && nums[low] <= pivot) low++;
if (low >= hight) break;
swap(nums, low, hight);
}
swap(nums,start,low);
return low;
}
public void insertSort (int[] nums, int low, int hight) {
for (int i = low+1; i <= hight; ++i) {
int temp = nums[i];
int j;
for (j = i-1; j >= 0; --j) {
if (temp < nums[j]) {
nums[j+1] = nums[j];
continue;
}
break;
}
nums[j+1] = temp;
}
}
public void swap (int[] nums, int i, int j) {
int temp = nums[i];
nums[i] = nums[j];
nums[j] = temp;
}
希尔排序
逐步分组进行粗调,再进行直接插入排序的思想,就是希尔排序,根据该算法的发明者,计算机科学家Donald Shell的名字所命名。示例中所使用的分组跨度,称为希尔排序的增量,增量的选择可以有很多种,在示例中所用的逐步折半的增量方法,是Donald Shell在发明希尔排序时提出的一种朴素方法,被称为希尔增量。
算法步骤
1.原始数组,{8,9,1,7,2,3,5,4,6,0},
2.初始增量gap=length/2=5,数组被分成5组:[8,3],[9,5],[1,4],[7,6],[2,0]
3.对这5组分别进行插入排序,然后缩小增量,gap=5/2=2,数组被分成两组[3,1,0,9,7][5,6,8,4,2]
4.对以上两组分别再进行插入排序,然后再缩小增量gap=2/2=1,此时整个数组为一组[0,2,1,4,3,5,7,6,9,8],
5.再进行排序
代码
示例1:
public static void main(String[] args) throws Exception {
int a[] = {2, 3, 54, 6};
//输出
System.out.println(Arrays.toString(sort(a)));
}
//
public static int[] sort(int[] sourceArray) throws Exception {
// 拷贝数组
int[] array = Arrays.copyOf(sourceArray, sourceArray.length);
//希尔排序的增量
int d = array.length;
while (d > 1) {
//使用希尔增量的方式,即每次折半
d = d / 2;
for (int x = 0; x < d; x++) {
for (int i = x + d; i < array.length; i = i + d) {
int temp = array[i];
int j;
for (j = i - d; j >= 0 && array[j] > temp; j = j - d) {
array[j + d] = array[j];
}
array[j + d] = temp;
}
}
}
return array;
}
示例2:
public static void main(String[] args) throws Exception {
int a[] = {2, 3, 54, 6};
//输出
int b[] = sort(a);
for (int i = 0; i < b.length; i++) {
System.out.println(b[i]);
}
}
public static int[] sort(int[] sourceArray) throws Exception {
// 对 arr 进行拷贝,不改变参数内容
int[] arr = Arrays.copyOf(sourceArray, sourceArray.length);
int gap = 1;
while (gap < arr.length) {
gap = gap * 3 + 1;
}
while (gap > 0) {
for (int i = gap; i < arr.length; i++) {
int tmp = arr[i];
int j = i - gap;
while (j >= 0 && arr[j] > tmp) {
arr[j + gap] = arr[j];
j -= gap;
}
arr[j + gap] = tmp;
}
gap = (int) Math.floor(gap / 3);
}
return arr;
}
时间复杂度
希尔排序的时间复杂度是O(n^2)。不稳定排序,值相同的元素可能被调换位置
快速排序
从数列中挑出一个元素,称为基准值(pivot)。排序数列,所有元素比基准值小的摆放在基准前面,所有元素比基准值大的摆在基准的后面(相同的数可以到任一边)。在这个分区退出之后,该基准就处于数列的中间位置。这个称为分区(partition)操作。递归地对【小于基准值元素的子数列】和【大于基准值元素的子数列】进行排序。
基本思想
- 先从数组中找一个基准数,比如就拿数组的第一个数为基准数。
- 把其他比它大的元素移动到数列一边,比他小的元素移动到数列另一边,从而把数组拆解成两个部分。
- 对左右区间重复第二步,直到各区间只有一个数。

优缺点
优点:性能较好,时间复杂度最好为O(nlogn),大多数场景性能都接近最优。原地排序,时间复杂度优于归并排序。缺点:部分场景,排序性能最差为O(n^2)。不稳定排序。
- 时间复杂度
快排是用递归来实现的,所以快速排序的性能取决于递归树的深度,如果每次分区操作,都能正好把数组分成大小接近相等的两个小区间,那么此时的递归树是平衡的,性能也较好,递归树的深度也就和归并排序求解方法一致。我们每一次分区需要对数组扫描一遍,做 n 次比较,所以最优情况下,快排的时间复杂度是 O(nlogn)。
- 空间复杂度
快速排序主要时递归造成的栈空间的使用,最好情况时其空间复杂度为O (logn),对应递归树的深度。最坏情况时则需要 n-1 次递归调用,此时空间复杂度为O(n)。
适用范围
大数据量且不要求排序稳定的场景。
场景优化
-
(1)避免选取最大、最小元素、第一个元素作基准值,采用三数取中法,随机选择三个数,取中间数为基准元素。
public int[] sortArray(int[] nums) { quickSort(nums,0,nums.length-1); return nums; } public void quickSort (int[] nums, int low, int hight) { if (low < hight) { int index = partition(nums,low,hight); quickSort(nums,low,index-1); quickSort(nums,index+1,hight); } } public int partition (int[] nums, int low, int hight) { //三数取中法 int mid = low + ((hight-low) >> 1); if (nums[low] > nums[hight]) swap(nums,low,hight); if (nums[mid] > nums[hight]) swap(nums,mid,hight); if (nums[mid] > nums[low]) swap(nums,mid,low); //下面和之前一样,仅仅是多了上面几行代码 int pivot = nums[low]; int start = low; while (low < hight) { while (low < hight && nums[hight] >= pivot) hight--; while (low < hight && nums[low] <= pivot) low++; if (low >= hight) break; swap(nums, low, hight); } swap(nums,start,low); return low; } public void swap (int[] nums, int i, int j) { int temp = nums[i]; nums[i] = nums[j]; nums[j] = temp; } -
(2)快排的性能优化双轴快排:2个基准数,例子:Arrays.sort() 。
代码示例
实现一:
public int[] sortArray(int[] nums) {
quickSort(nums,0,nums.length-1);
return nums;
}
public void quickSort (int[] nums, int low, int hight) {
if (low < hight) {
//分区,获取分区后的基准值index,采用递归方式,不断缩小排序范围
int index = partition(nums,low,hight);
//左分区,从第一位开始到基准值的前一位
quickSort(nums,low,index-1);
//右分区,从基准值后一位开始到最后一位
quickSort(nums,index+1,hight);
}
}
public int partition (int[] nums, int low, int hight) {
//取数组第一个数作为基准值
int pivot = nums[low];
//排序值至少要有3个数值,如果只有两个的话不需要排序
while (low < hight) {
//从数组最后面一个数开始,依次往前取值,直到等于基准值的坐标为止,找到小于基准值的数
while (low < hight && nums[hight] >= pivot) {
hight--;
}
//如果当前对比值的坐标大于基准值坐标,则把小于基准值的数放到左边
if (low < hight) nums[low] = nums[hight];
//从数组第一个数开始,依次往后对比,直到等于基准值为止,找到大于基准值的数
while (low < hight && nums[low] <= pivot) {
low++;
}
//把大于基准值的数放到右边
if (low < hight) nums[hight] = nums[low];
}
//基准数放到合适的位置
nums[low] = pivot;
return low;
}
实现二:
public static void main(String[] args) {
int a[] = {2, 3, 54, 6};
// 对数组a进行拷贝,不改变参数内容
int[] arr = Arrays.copyOf(a, a.length);
quickSort(arr, 0, arr.length - 1);
for (int i = 0; i < arr.length; i++) {
System.out.println(arr[i]);
}
}
private static int[] quickSort(int[] arr, int left, int right) {
if (left < right) {
int partitionIndex = partition(arr, left, right);
quickSort(arr, left, partitionIndex - 1);
quickSort(arr, partitionIndex + 1, right);
}
return arr;
}
private static int partition(int[] arr, int left, int right) {
// 设定基准值(pivot)
int pivot = left;
int index = pivot + 1;
for (int i = index; i <= right; i++) {
if (arr[i] < arr[pivot]) {
swap(arr, i, index);
index++;
}
}
swap(arr, pivot, index - 1);
return index - 1;
}
private static void swap(int[] arr, int i, int j) {
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
快速排序的迭代写法(用栈来实现)
利用了先进先出的特性,分区跟上面一致,关注入栈出栈情况即可。
public int[] sortArray(int[] nums) {
Stack<Integer> stack = new Stack<>();
stack.push(nums.length - 1);
stack.push(0);
while (!stack.isEmpty()) {
int low = stack.pop();
int hight = stack.pop();
if (low < hight) {
int index = partition(nums, low, hight);
stack.push(index - 1);
stack.push(low);
stack.push(hight);
stack.push(index + 1);
}
}
return nums;
}
public int partition (int[] nums, int low, int hight) {
int pivot = nums[low];
int start = low;
while (low < hight) {
while (low < hight && nums[hight] >= pivot) hight--;
while (low < hight && nums[low] <= pivot) low++;
if (low >= hight) break;
swap(nums, low, hight);
}
swap(nums,start,low);
return low;
}
public void swap (int[] nums, int i, int j) {
int temp = nums[i];
nums[i] = nums[j];
nums[j] = temp;
}
if后面加与不加{}问题
1.不加{}
if (1==2)
x=1;y=2;z=3;
编译后
if (1==2)
{x=1};y=2;z=3;
所以当1!=2时,y=2;z=3;仍执行。
2.加{}
if (1 == 2)
{ x=1;y=2;z=3;}
所以当1!=2时,都不执行。
通俗理解:后面不加{}时,就近原则,只控制第一句
归并排序
归并排序是建立在归并操作上的一种有效的排序算法。该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为2-路归并。

算法步骤
- 申请空间,使其大小为两个已经排序序列之和,该空间用来存放合并后的序列;
- 设定两个指针,最初位置分别为两个已经排序序列的起始位置;
- 比较两个指针所指向的元素,选择相对小的元素放入到合并空间,并移动指针到下一位置;
- 重复步骤 3 直到某一指针达到序列尾;
- 将另一序列剩下的所有元素直接复制到合并序列尾
优缺点
优点:性能好且稳定,时间复杂度为O(nlogn) 。稳定排序,适用场景更多。缺点:非原地排序,空间复杂度高。
适用范围
大数据量且期望要求排序稳定的场景。
代码示例
public static void main(String[] args) throws Exception {
int a[] = {2, 3, 54, 6};
//输出
int b[] = sort(a);
for (int i = 0; i < b.length; i++) {
System.out.println(b[i]);
}
}
public static int[] sort(int[] sourceArray) throws Exception {
// 对 arr 进行拷贝,不改变参数内容
int[] arr = Arrays.copyOf(sourceArray, sourceArray.length);
if (arr.length < 2) {
return arr;
}
int middle = (int) Math.floor(arr.length / 2);
int[] left = Arrays.copyOfRange(arr, 0, middle);
int[] right = Arrays.copyOfRange(arr, middle, arr.length);
return merge(sort(left), sort(right));
}
protected static int[] merge(int[] left, int[] right) {
int[] result = new int[left.length + right.length];
int i = 0;
while (left.length > 0 && right.length > 0) {
if (left[0] <= right[0]) {
result[i++] = left[0];
left = Arrays.copyOfRange(left, 1, left.length);
} else {
result[i++] = right[0];
right = Arrays.copyOfRange(right, 1, right.length);
}
}
while (left.length > 0) {
result[i++] = left[0];
left = Arrays.copyOfRange(left, 1, left.length);
}
while (right.length > 0) {
result[i++] = right[0];
right = Arrays.copyOfRange(right, 1, right.length);
}
return result;
}
计数排序
不是基于比较的排序算法,其核心在于将输入的数据值转化为键存储在额外开辟的数组空间中。 作为一种线性时间复杂度的排序,计数排序要求输入的数据必须是有确定范围的整数。 算法描述。

算法步骤
- 用O(n)的时间扫描整个序列A,获取最小值min和最大值max
- 创建新的数组B,长度为(max - min + 1)
- 数组B中index的元素记录的值是A中某元素出现的次数
- 最后输出目标整数序列,具体的逻辑是遍历数组B,输出相应元素以及对应的个数
优缺点
优点:性能比快速查询要好很多,时间复杂度为O(n+k),k为数列最大值。稳定排序。缺点:适用范围比较狭窄。
适用范围
数列元素是整数,当k不是很大且序列比较集中时适用。
场景优化
数字不是从0开始,会存在空间浪费的问题 数列的最小值作为偏移量,以数列最大值-最小值+1作为统计数组的长度。
代码示例
public static void main(String[] args) {
int a[] = {2, 3, 54, 6};
// 对数组a进行拷贝,不改变参数内容
int[] arr = Arrays.copyOf(a, a.length);
int maxValue = getMaxValue(arr);
countingSort(arr, maxValue);
for (int i = 0; i < arr.length; i++) {
System.out.println(arr[i]);
}
}
private static int[] countingSort(int[] arr, int maxValue) {
int bucketLen = maxValue + 1;
int[] bucket = new int[bucketLen];
for (int value : arr) {
bucket[value]++;
}
int sortedIndex = 0;
for (int j = 0; j < bucketLen; j++) {
while (bucket[j] > 0) {
arr[sortedIndex++] = j;
bucket[j]--;
}
}
return arr;
}
private static int getMaxValue(int[] arr) {
int maxValue = arr[0];
for (int value : arr) {
if (maxValue < value) {
maxValue = value;
}
}
return maxValue;
} 
堆排序
堆排序(Heapsort)是指利用堆这种数据结构所设计的一种排序算法。堆积是一个近似完全二叉树的结构,并同时满足堆积的性质:即子结点的键值或索引总是小于(或者大于)它的父节点。

算法步骤
- 创建一个堆 H[0……n-1]
- 把堆首(最大值)和堆尾互换
- 把堆的尺寸缩小1,并调用shift_down(0),目的是把新的数组顶端数据调整到相应位置。
- 重复步骤2,直到堆的尺寸为1。
优缺点
优点:性能较好,时间复杂度为O(nlogn)。时间复杂度比较稳定。辅助空间复杂度为O(1)。缺点:数据变动的情况下,堆的维护成本较高。
适用范围
数据量大且数据呈流式输入的场景。
为什么实际情况快排比堆排快堆排序的过程可知,建立最大堆后,会将堆顶的元素和最后一个元素对调,然后让那最后一个元素从顶上往下沉到恰当的位置,因为底部的元素一定是比较小的,下沉的过程中会进行大量的近乎无效的比较。所以堆排虽然和快排一样复杂度都是O(NlogN),但堆排复杂度的常系数更大。

代码示例
public static void main(String[] args) {
int a[] = {2, 3, 54, 6};
// 对 arr 进行拷贝,不改变参数内容
int[] arr = Arrays.copyOf(a, a.length);
int len = arr.length;
buildMaxHeap(arr, len);
for (int i = len - 1; i > 0; i--) {
swap(arr, 0, i);
len--;
heapify(arr, 0, len);
}
//输出
for (int i = 0; i < arr.length; i++) {
System.out.println(arr[i]);
}
}
private static void buildMaxHeap(int[] arr, int len) {
for (int i = (int) Math.floor(len / 2); i >= 0; i--) {
heapify(arr, i, len);
}
}
private static void heapify(int[] arr, int i, int len) {
int left = 2 * i + 1;
int right = 2 * i + 2;
int largest = i;
if (left < len && arr[left] > arr[largest]) {
largest = left;
}
if (right < len && arr[right] > arr[largest]) {
largest = right;
}
if (largest != i) {
swap(arr, i, largest);
heapify(arr, largest, len);
}
}
private static void swap(int[] arr, int i, int j) {
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
桶排序
桶排序是计数排序的升级版。它利用了函数的映射关系,高效与否的关键就在于这个映射函数的确定。桶排序 (Bucket sort)的工作的原理:假设输入数据服从均匀分布,将数据分到有限数量的桶里,每个桶再分别排序(有可能再使用别的排序算法或是以递归方式继续使用桶排序进行排)。

算法步骤
- 设置固定数量的空桶。
- 把数据放到对应的桶中。
- 对每个不为空的桶中数据进行排序。
- 拼接不为空的桶中数据,得到结果
优缺点
优点:最优时间复杂度为O(n),完爆比较排序算法。缺点:适用范围比较狭窄。时间复杂度不稳定。
适用范围
数据服从均匀分布的场景。
代码示例
private static final InsertSort insertSort = new InsertSort();//插入排序对象
public static void main(String[] args) throws Exception {
int a[] = {2, 3, 54, 6};
//输出
int b[] = sort(a);
for (int i = 0; i < b.length; i++) {
System.out.println(b[i]);
}
}
public static int[] sort(int[] sourceArray) throws Exception {
// 对 arr 进行拷贝,不改变参数内容
int[] arr = Arrays.copyOf(sourceArray, sourceArray.length);
return bucketSort(arr, 5);
}
private static int[] bucketSort(int[] arr, int bucketSize) throws Exception {
if (arr.length == 0) {
return arr;
}
int minValue = arr[0];
int maxValue = arr[0];
for (int value : arr) {
if (value < minValue) {
minValue = value;
} else if (value > maxValue) {
maxValue = value;
}
}
int bucketCount = (int) Math.floor((maxValue - minValue) / bucketSize) + 1;
int[][] buckets = new int[bucketCount][0];
// 利用映射函数将数据分配到各个桶中
for (int i = 0; i < arr.length; i++) {
int index = (int) Math.floor((arr[i] - minValue) / bucketSize);
buckets[index] = arrAppend(buckets[index], arr[i]);
}
int arrIndex = 0;
for (int[] bucket : buckets) {
if (bucket.length <= 0) {
continue;
}
// 对每个桶进行排序,这里使用了插入排序,调用一个插入排序的方法
bucket = insertSort.sort(bucket);
for (int value : bucket) {
arr[arrIndex++] = value;
}
}
return arr;
}
//自动扩容,并保存数据
private static int[] arrAppend(int[] arr, int value) {
arr = Arrays.copyOf(arr, arr.length + 1);
arr[arr.length - 1] = value;
return arr;
}
基数排序
- 将所有待比较数值(正整数)统一为同样的数位长度,数位较短的数前面补零
- 从最低位开始,依次进行一次排序
- 从最低位排序一直到最高位排序完成以后, 数列就变成一个有序序列
代码
public static void main(String[] args) throws Exception {
int a[] = {2, 3, 54, 6};
//输出
int b[] = sort(a);
for (int i = 0; i < b.length; i++) {
System.out.println(b[i]);
}
}
public static int[] sort(int[] sourceArray) throws Exception {
// 对 arr 进行拷贝,不改变参数内容
int[] arr = Arrays.copyOf(sourceArray, sourceArray.length);
int maxDigit = getMaxDigit(arr);
return radixSort(arr, maxDigit);
}
// 获取最高位数
private static int getMaxDigit(int[] arr) {
int maxValue = getMaxValue(arr);
return getNumLenght(maxValue);
}
private static int getMaxValue(int[] arr) {
int maxValue = arr[0];
for (int value : arr) {
if (maxValue < value) {
maxValue = value;
}
}
return maxValue;
}
protected static int getNumLenght(long num) {
if (num == 0) {
return 1;
}
int lenght = 0;
for (long temp = num; temp != 0; temp /= 10) {
lenght++;
}
return lenght;
}
private static int[] radixSort(int[] arr, int maxDigit) {
int mod = 10;
int dev = 1;
for (int i = 0; i < maxDigit; i++, dev *= 10, mod *= 10) {
// 考虑负数的情况,这里扩展一倍队列数,其中 [0-9]对应负数,[10-19]对应正数 (bucket + 10)
int[][] counter = new int[mod * 2][0];
for (int j = 0; j < arr.length; j++) {
int bucket = ((arr[j] % mod) / dev) + mod;
counter[bucket] = arrayAppend(counter[bucket], arr[j]);
}
int pos = 0;
for (int[] bucket : counter) {
for (int value : bucket) {
arr[pos++] = value;
}
}
}
return arr;
}
private static int[] arrayAppend(int[] arr, int value) {
arr = Arrays.copyOf(arr, arr.length + 1);
arr[arr.length - 1] = value;
return arr;
}
CAS
CAS:Compare and Swap,即比较再交换。jdk5增加了并发包java.util.concurrent.*,其下面的类使用CAS算法实现了区别于synchronouse同步锁的一种乐观锁。JDK 5之前Java语言是靠synchronized关键字保证同步的,这是一种独占锁,也是是悲观锁。
对CAS算法理解
CAS是一种无锁算法,CAS有3个操作数,内存值V,旧的预期值A,要修改的新值B。当且仅当预期值A和内存值V相同时,将内存值V修改为B,否则什么都不做。
CAS比较与交换的伪代码可以表示为:
do{
备份旧数据;
基于旧数据构造新数据;
}while(!CAS( 内存地址,备份的旧数据,新数据 ))
注:t1,t2线程是同时更新同一变量56的值 因为t1和t2线程都同时去访问同一变量56,所以他们会把主内存的值完全拷贝一份到自己的工作内存空间,所以t1和t2线程的预期值都为56。 假设t1在与t2线程竞争中线程t1能去更新变量的值,而其他线程都失败。(失败的线程并不会被挂起,而是被告知这次竞争中失败,并可以再次发起尝试)。t1线程去更新变量值改为57,然后写到内存中。此时对于t2来说,内存值变为了57,与预期值56不一致,就操作失败了(想改的值不再是原来的值)。 (上图通俗的解释是:CPU去更新一个值,但如果想改的值不再是原来的值,操作就失败,因为很明显,有其它操作先改变了这个值。) 就是指当两者进行比较时,如果相等,则证明共享数据没有被修改,替换成新值,然后继续往下运行;如果不相等,说明共享数据已经被修改,放弃已经所做的操作,然后重新执行刚才的操作。容易看出 CAS 操作是基于共享数据不会被修改的假设,采用了类似于数据库的commit-retry 的模式。当同步冲突出现的机会很少时,这种假设能带来较大的性能提升。
CAS开销
CAS(比较并交换)是CPU指令级的操作,只有一步原子操作,所以非常快。而且CAS避免了请求操作系统来裁定锁的问题,不用麻烦操作系统,直接在CPU内部就搞定了。但CAS就没有开销了吗?不!有cache miss的情况。这个问题比较复杂,首先需要了解CPU的硬件体系结构: 一个8核CPU计算机系统,每个CPU有cache(CPU内部的高速缓存,寄存器),管芯内还带有一个互联模块,使管芯内的两个核可以互相通信。在图中央的系统互联模块可以让四个管芯相互通信,并且将管芯与主存连接起来。数据以“缓存线”为单位在系统中传输,“缓存线”对应于内存中一个 2 的幂大小的字节块,大小通常为 32 到 256 字节之间。当 CPU 从内存中读取一个变量到它的寄存器中时,必须首先将包含了该变量的缓存线读取到 CPU 高速缓存。同样地,CPU 将寄存器中的一个值存储到内存时,不仅必须将包含了该值的缓存线读到 CPU 高速缓存,还必须确保没有其他 CPU 拥有该缓存线的拷贝。 比如,如果 CPU0 在对一个变量执行“比较并交换”(CAS)操作,而该变量所在的缓存线在 CPU7 的高速缓存中,就会发生以下经过简化的事件序列:
CPU0 检查本地高速缓存,没有找到缓存线。
请求被转发到 CPU0 和 CPU1 的互联模块,检查 CPU1 的本地高速缓存,没有找到缓存线。
请求被转发到系统互联模块,检查其他三个管芯,得知缓存线被 CPU6和 CPU7 所在的管芯持有。
请求被转发到 CPU6 和 CPU7 的互联模块,检查这两个 CPU 的高速缓存,在 CPU7 的高速缓存中找到缓存线。
CPU7 将缓存线发送给所属的互联模块,并且刷新自己高速缓存中的缓存线。
CPU6 和 CPU7 的互联模块将缓存线发送给系统互联模块。
系统互联模块将缓存线发送给 CPU0 和 CPU1 的互联模块。
CPU0 和 CPU1 的互联模块将缓存线发送给 CPU0 的高速缓存。
CPU0 现在可以对高速缓存中的变量执行 CAS 操作了
以上是刷新不同CPU缓存的开销。最好情况下的 CAS 操作消耗大概 40 纳秒,超过 60 个时钟周期。这里的“最好情况”是指对某一个变量执行 CAS 操作的 CPU 正好是最后一个操作该变量的CPU,所以对应的缓存线已经在 CPU 的高速缓存中了,类似地,最好情况下的锁操作(一个“round trip 对”包括获取锁和随后的释放锁)消耗超过 60 纳秒,超过 100 个时钟周期。这里的“最好情况”意味着用于表示锁的数据结构已经在获取和释放锁的 CPU 所属的高速缓存中了。锁操作比 CAS 操作更加耗时,是因深入理解并行编程 为锁操作的数据结构中需要两个原子操作。缓存未命中消耗大概 140 纳秒,超过 200 个时钟周期。需要在存储新值时查询变量的旧值的 CAS 操作,消耗大概 300 纳秒,超过 500 个时钟周期。想想这个,在执行一次 CAS 操作的时间里,CPU 可以执行 500 条普通指令。这表明了细粒度锁的局限性。
CAS算法在JDK中的应用
在原子类变量中,如java.util.concurrent.atomic中的AtomicXXX,都使用了这些底层的JVM支持为数字类型的引用类型提供一种高效的CAS操作,而在java.util.concurrent中的大多数类在实现时都直接或间接的使用了这些原子变量类










