1.向量范数和矩阵范数
1.1 向量范数
向量范数描述向量在空间中的大小
下图来自:范数(简单的理解)、范数的用途、什么是范数

1.1.1 曼哈顿距离(Manhattan Distance)或 L 1 L_1 L1范数( p = 1 p=1 p=1 )

1-范数单位圆(红线上所有点的曼哈顿距离都为1)

1.1.2 欧式距离(Euclidean Distance)或 L 2 L_2 L2范数( p = 2 p=2 p=2 )

2-范数单位圆(红线上所有点的欧式距离都为1)

1.1.3 L p L_{p} Lp 范数、 L ∞ L_{\infty} L∞范数
L
p
=
(
∑
i
=
1
k
∣
x
i
∣
p
)
1
p
L_{p}=\bigg(\sum_{i=1}^k|x_i|^p\bigg)^{\frac{1}{p}}
Lp=(i=1∑k∣xi∣p)p1

下图中从
p
=
4
p=4
p=4 到
p
=
∞
p=\infty
p=∞
截图来源:What is Norm in Machine Learning?
1.2 矩阵范数
矩阵范数描述矩阵引起变化的大小
笔记来源:Matrix Norms


1.2.1 矩阵1-范数( p = 1 p=1 p=1 )


1.2.2 矩阵2-范数( p = 2 p=2 p=2)

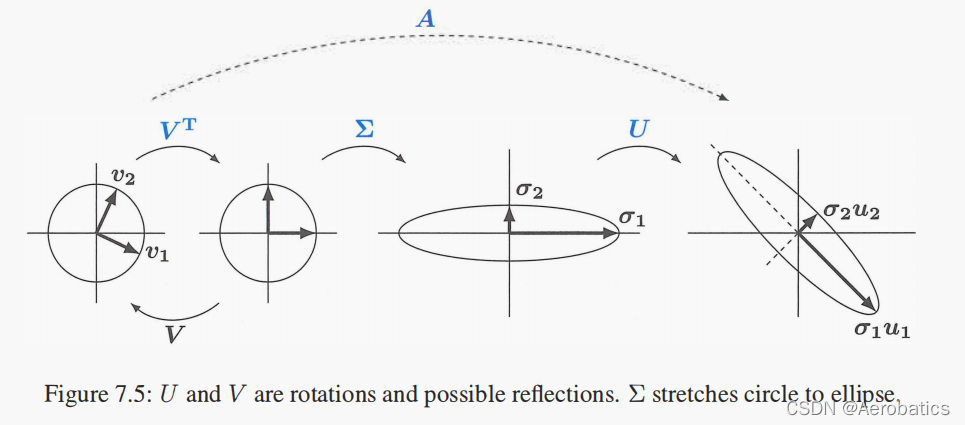
奇异值分解(SVD)
A
=
U
Σ
V
T
A=U\Sigma V^T
A=UΣVT

A
v
1
=
σ
1
u
1
A
v
2
=
σ
2
u
2
A\boldsymbol{v}_1=\sigma_1\boldsymbol{u}_1\\ A\boldsymbol{v}_2=\sigma_2\boldsymbol{u}_2
Av1=σ1u1Av2=σ2u2
范数的应用之一:
均方差(Mean Square Error)


1.2.3 矩阵 ∞ \infty ∞-范数( p = ∞ p=\infty p=∞)

1.2.1 Frobenius范数
矩阵的每个元素的平方和的开方

