题目

给你一个大小为 m x n 的二进制矩阵 grid ，其中 0 表示一个海洋单元格、1 表示一个陆地单元格。

一次 移动 是指从一个陆地单元格走到另一个相邻（上、下、左、右）的陆地单元格或跨过 grid 的边界。

返回网格中 无法 在任意次数的移动中离开网格边界的陆地单元格的数量。

示例 1：

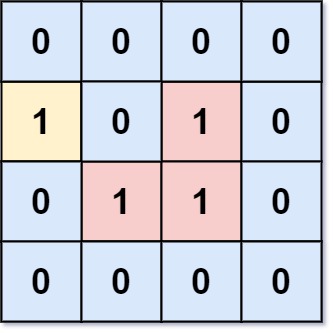
输入：grid = [[0,0,0,0],[1,0,1,0],[0,1,1,0],[0,0,0,0]]
输出：3
解释：有三个 1 被 0 包围。一个 1 没有被包围，因为它在边界上。
示例 2：

输入：grid = [[0,1,1,0],[0,0,1,0],[0,0,1,0],[0,0,0,0]]
输出：0
解释：所有 1 都在边界上或可以到达边界。

提示：

m == grid.length
n == grid[i].length
1 <= m, n <= 500
grid[i][j] 的值为 0 或 1

正解

链接

自解

class Solution {
public:
    struct point {
        int i,j;
        point(int i,int j) : i(i), j(j) {};
    };

    int numEnclaves(vector<vector<int>>& grid) { //多源搜索
        int landamount = 0;
        queue<point> buf;

        for(int i=0;i<grid.size();i++) {
            for(int j=0;j<grid[0].size();j++) {
                // cout << grid[i][j];
                if(grid[i][j]==1) {
                    
                    if(i == 0 || i == grid.size()-1 || j == 0 || j == grid[0].size() - 1) {
                        buf.push(point(i, j));
                        grid[i][j] = 0;
                    }
                    else {
                        landamount++;
                    }
                }
                
            }
            // cout << endl;
        }
// cout << endl;
        while(!buf.empty()) {
            point tmp = buf.front();
            buf.pop();
            
            

            if(tmp.i + 1 < grid.size() && grid[tmp.i+1][tmp.j] == 1) {
                buf.push(point(tmp.i + 1, tmp.j));
                grid[tmp.i+1][tmp.j] = 0;
                landamount--;
            }
            if(tmp.i - 1 >= 0 && grid[tmp.i-1][tmp.j] == 1) {
                buf.push(point(tmp.i - 1, tmp.j));
                grid[tmp.i-1][tmp.j] = 0;
                landamount--;
            }
            if(tmp.j + 1 < grid[0].size() && grid[tmp.i][tmp.j + 1] == 1) {
                buf.push(point(tmp.i, tmp.j + 1));
                grid[tmp.i][tmp.j+ 1] = 0;
                landamount--;
            }
            if(tmp.j - 1 >= 0 && grid[tmp.i][tmp.j - 1] == 1) {
                buf.push(point(tmp.i, tmp.j - 1));
                grid[tmp.i][tmp.j- 1] = 0;
                landamount--;
            }


        }

        // for(int i=0;i<grid.size();i++) {
        //     for(int j=0;j<grid[0].size();j++) {
        //         cout << grid[i][j];
        //         if(grid[i][j]==1) {
                    
                    
        //             landamount++;
 
        //         }
                
        //     }
        //     cout << endl;
        // }

        return landamount;

    }
};