题目描述
给你一个大小为 m x n 的二进制矩阵 grid ,其中 0 表示一个海洋单元格、1 表示一个陆地单元格。
一次 移动 是指从一个陆地单元格走到另一个相邻(上、下、左、右)的陆地单元格或跨过 grid 的边界。
返回网格中 无法 在任意次数的移动中离开网格边界的陆地单元格的数量。
示例 1:
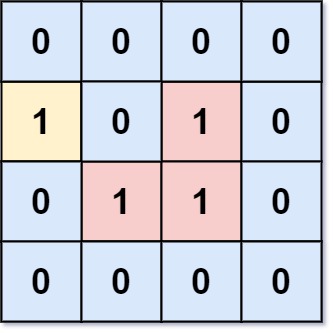
输入:grid = [[0,0,0,0],[1,0,1,0],[0,1,1,0],[0,0,0,0]]
输出:3
解释:有三个 1 被 0 包围。一个 1 没有被包围,因为它在边界上。
示例 2:
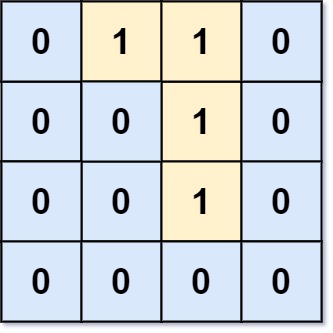
输入:grid = [[0,1,1,0],[0,0,1,0],[0,0,1,0],[0,0,0,0]]
输出:0
解释:所有 1 都在边界上或可以到达边界。
提示:
m == grid.length
n == grid[i].length
1 <= m, n <= 500
grid[i][j] 的值为 0 或 1
思路:
创建一个新的二维数组arr,用于存储能够走出边界的陆地,将对应的坐标置为1。最后将grid中1的总量减去arr中1的总量得到的结果即为飞地的数量。
此时题目化为寻找能走出边界的陆地,即我们从边界开始寻找为1的陆地,然后将对应的arr置为1,然后继续向矩形内部寻找,遍历其四面的陆地(grid[i][j]=1)并且没有走过的陆地(arr[i][j]=0)的情况,然后逐渐递归解决
代码
class Solution {
public static int numEnclaves(int[][] grid) {
int m= grid.length;
int n=grid[1].length;
int[][] arr=new int[m][n]; //存储能够走出边界的位置为1;
for(int i=0;i<n;i++){ //第一行
if(grid[0][i]==1){
arr[0][i]=1;
if(m>=2&&grid[1][i]==1&&arr[1][i]!=1){
arr[1][i]=1;
fun(grid,arr,1,i,m,n);
}
}
}
for(int i=0;i<n;i++){ //最后一行
if(grid[m-1][i]==1){
arr[m-1][i]=1;
if(m-2>=0&&grid[m-2][i]==1&&arr[m-2][i]!=1){
arr[m-2][i]=1;
fun(grid,arr,m-2,i,m,n);
}
}
}
for(int i=0;i<m;i++){ //第一列
if(grid[i][0]==1){
arr[i][0]=1;
if(n>=2&&grid[i][1]==1&&arr[i][1]!=1){
arr[i][1]=1;
fun(grid,arr,i,1,m,n);
}
}
}
for(int i=0;i<m;i++){ //最后一列
if(grid[i][n-1]==1){
arr[i][n-1]=1;
if(n-2>=0&&grid[i][n-2]==1&&arr[i][n-2]!=1){
arr[i][n-2]=1;
fun(grid,arr,i,n-2,m,n);
}
}
}
int arrsum=0;
for(int i=0;i<m;i++){
for(int j=0;j<n;j++){
if(arr[i][j]==1){
arrsum++;
}
}
}
int gridsum=0;
for(int i=0;i<m;i++){
for(int j=0;j<n;j++){
if(grid[i][j]==1){
gridsum++;
}
}
}
return gridsum-arrsum;
}
public static void fun(int[][] grid, int[][] arr, int a, int b,int m,int n){
if(a-1>=0&&grid[a-1][b]==1&&arr[a-1][b]!=1){
//传入坐标位置的上方为1且未被计入arr中
arr[a-1][b]=1;
fun(grid, arr, a-1, b,m,n);
}
if(a+1<m&&grid[a+1][b]==1&&arr[a+1][b]!=1){
//传入坐标位置的下方为1且未被计入arr中
arr[a+1][b]=1;
fun(grid, arr, a+1, b,m,n);
}
if(b-1>=0&&grid[a][b-1]==1&&arr[a][b-1]!=1){
//传入坐标位置的左方为1且未被计入arr中
arr[a][b-1]=1;
fun(grid, arr, a, b-1,m,n);
}
if(b+1<n&&grid[a][b+1]==1&&arr[a][b+1]!=1){
//传入坐标位置的右方为1且未被计入arr中
arr[a][b+1]=1;
fun(grid, arr, a, b+1,m,n);
}
}
}









