从前序与中序遍历序列构造二叉树(树、数组)
给定一棵树的前序遍历 preorder 与中序遍历 inorder。请构造二叉树并返回其根节点。
示例 1:
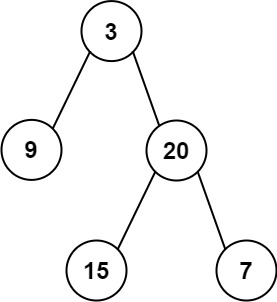Input: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7] Output: [3,9,20,null,null,15,7]
示例 2:
Input: preorder = [-1], inorder = [-1] Output: [-1]
提示:
- 1 <= preorder.length <= 3000
- inorder.length == preorder.length
- -3000 <= preorder[i], inorder[i] <= 3000
- preorder 和 inorder 均无重复元素
- inorder 均出现在 preorder
- preorder 保证为二叉树的前序遍历序列
- inorder 保证为二叉树的中序遍历序列
解答：
public class TreeNode {
int val;
TreeNode left;
TreeNode right;
TreeNode(int x) {
val = x;
}
}
public class Solution {
public TreeNode buildTree(int[] preorder, int[] inorder) {
if (preorder.length != inorder.length)
return null;
if (preorder.length == 0)
return null;
if (preorder.length == 1)
return new TreeNode(preorder[0]);
return buildTree(preorder, inorder, 0, preorder.length - 1, 0, inorder.length - 1);
}
private TreeNode buildTree(int[] preorder, int[] inorder, int prei, int prej, int ini, int inj) {
if (prei > prej || ini > inj || prei < 0 || prej >= preorder.length || ini < 0 || inj >= inorder.length)
return null;
if (prej - prei < 0)
return null;
if (prei == prej)
return new TreeNode(preorder[prei]);
TreeNode root = new TreeNode(preorder[prei]);
int inFlag = 0;
for (int i = ini; i <= inj; i++) {
if (inorder[i] == root.val) {
inFlag = i;
break;
}
}
int num_left = inFlag - ini;
int num_right = inj - inFlag;
root.left = buildTree(preorder, inorder, prei + 1, prei + num_left, ini, inFlag - 1);
root.right = buildTree(preorder, inorder, prej - num_right + 1, prej, inFlag + 1, inj);
return root;
}
}
K 个一组翻转链表(递归、链表)
给你一个链表，每 _k _个节点一组进行翻转，请你返回翻转后的链表。 _k _是一个正整数，它的值小于或等于链表的长度。 如果节点总数不是 _k _的整数倍，那么请将最后剩余的节点保持原有顺序。 进阶：
- 你可以设计一个只使用常数额外空间的算法来解决此问题吗？
- 你不能只是单纯的改变节点内部的值，而是需要实际进行节点交换。
示例 1：
输入：head = [1,2,3,4,5], k = 2
输出：[2,1,4,3,5]
示例 2：
输入：head = [1,2,3,4,5], k = 3
输出：[3,2,1,4,5]
示例 3：
输入：head = [1,2,3,4,5], k = 1
输出：[1,2,3,4,5]
示例 4：
输入：head = [1], k = 1
输出：[1]
提示：
- 列表中节点的数量在范围 sz 内
- 1 <= sz <= 5000
- 0 <= Node.val <= 1000
- 1 <= k <= sz
以下程序实现了这一功能，请你填补空白处内容：
解答：
public class ListNode {
int val;
ListNode next;
ListNode() {
}
ListNode(int val) {
this.val = val;
}
ListNode(int val, ListNode next) {
this.val = val;
this.next = next;
}
}
class Solution {
public ListNode reverseKGroup(ListNode head, int k) {
if (head == null) {
return null;
}
ListNode a = head, b = head;
for (int i = 0; i < k; i++) {
if (b == null) {
return a;
}
b = b.next;
}
ListNode newHead = reverse(a, b);
a.next = reverseKGroup(b, k);
return newHead;
}
public ListNode reverse(ListNode a, ListNode b) {
ListNode pre, cur, nxt;
pre = null;
cur = a;
nxt = a;
while (nxt != b) {
__________________;
}
return pre;
}
}
解答：
nxt = cur.next;
cur.next = pre;
pre = cur;
cur = nxt;
完美矩形(数组、扫描线)
我们有 N 个与坐标轴对齐的矩形, 其中 N > 0, 判断它们是否能精确地覆盖一个矩形区域。
每个矩形用左下角的点和右上角的点的坐标来表示。例如， 一个单位正方形可以表示为 [1,1,2,2]。 ( 左下角的点的坐标为 (1, 1) 以及右上角的点的坐标为 (2, 2) )。
示例 1:
rectangles = [ [1,1,3,3], [3,1,4,2], [3,2,4,4], [1,3,2,4], [2,3,3,4] ]
返回 true。5个矩形一起可以精确地覆盖一个矩形区域。
rectangles = [ [1,1,2,3], [1,3,2,4], [3,1,4,2], [3,2,4,4] ]
返回 false。两个矩形之间有间隔，无法覆盖成一个矩形。
rectangles = [ [1,1,3,3], [3,1,4,2], [1,3,2,4], [3,2,4,4] ]
返回 false。图形顶端留有间隔，无法覆盖成一个矩形。
rectangles = [ [1,1,3,3], [3,1,4,2], [1,3,2,4], [2,2,4,4] ]
返回 false。因为中间有相交区域，虽然形成了矩形，但不是精确覆盖。
解答：
class Solution {
public boolean isRectangleCover(int[][] rectangles) {
int left = Integer.MAX_VALUE;
int right = Integer.MIN_VALUE;
int top = Integer.MIN_VALUE;
int bottom = Integer.MAX_VALUE;
int n = rectangles.length;
Set<String> set = new HashSet<>();
int sumArea = 0;
for (int i = 0; i < n; i++) {
left = Math.min(left, rectangles[i][0]);
bottom = Math.min(bottom, rectangles[i][1]);
right = Math.max(right, rectangles[i][2]);
top = Math.max(top, rectangles[i][3]);
sumArea += (rectangles[i][3] - rectangles[i][1]) * (rectangles[i][2] - rectangles[i][0]);
String lt = rectangles[i][0] + " " + rectangles[i][3];
String lb = rectangles[i][0] + " " + rectangles[i][1];
String rt = rectangles[i][2] + " " + rectangles[i][3];
String rb = rectangles[i][2] + " " + rectangles[i][1];
if (!set.contains(lt))
set.add(lt);
else
set.remove(lt);
if (!set.contains(lb))
set.add(lb);
else
set.remove(lb);
if (!set.contains(rt))
set.add(rt);
else
set.remove(rt);
if (!set.contains(rb))
set.add(rb);
else
set.remove(rb);
}
if (set.size() == 4 && set.contains(left + " " + top) && set.contains(left + " " + bottom)
&& set.contains(right + " " + bottom) && set.contains(right + " " + top)) {
return sumArea == (right - left) * (top - bottom);
}
return false;
}
}
本文内容到此结束了， 如有收获欢迎点赞👍收藏💖关注✔️，您的鼓励是我最大的动力。 如有错误❌疑问💬欢迎各位大佬指出。 主页：共饮一杯无的博客汇总👨💻
保持热爱，奔赴下一场山海。🏃🏃🏃
