目录
13.1 欧拉图与中国邮递员问题
13.1.1 欧拉图基本知识点
1）欧拉道路（回路）的定义：
2）如何判别欧拉图：具有欧拉回路的图
3）一个图含有欧拉道路的条件：
4）连通有向图G中含有有向欧拉道路和回路的充要条件
13.1.2 Fleury算法（构造欧拉回路）
注：如果
是割边，同时还有其他边与
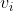相关联，则不能选
13.1.3 中国邮递员问题算法
（1）若G不含奇数度结点，则任一欧拉回路就是问题的解决
（2）若G含有2K（K>0）个奇数度结点，则先求出其中任何两点间的最短路径，然后再在这些路径之中找出K条路径P1，P2,...,Pk，使得满足以下条件：
①任何Pi和Pj（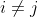
）没有相同的起点和终点
②在所满足①的K条最短路径的集合中，P1,P2,...,Pk的长度总和最短
（3）根据（2）中求出的K条最短道路P1,P2,...,Pk，在原图G中复制所有出现的在这条道路上的边，设所得之图为G'。
（4）构造G'的欧拉回路，即得中国邮递员问题的解。
13.2 哈密顿图与推销商问题
13.2.1 哈密顿图
1）哈密顿道路（圈）的定义：
2）判断是否是哈密顿图的必要条件：
3）判断是否是哈密顿图的充分条件：
13.2.2 推销商问题
⭐图的闭包
定义：设G=<V,E>是n阶的简单图。若存在一对不相邻的结点
，满足：
则构造图G+uv，并且在图上G+uv重复上述步骤，直至不再存在这样的结点对为止，所得之图称为图G的闭包，记为c(G)。
（让所有满足的两点相邻）
定理：一个简单图G是哈密顿图当且仅当其闭包图是哈密顿图
